Fractale 3D

Réaliser des figures voir des film en 3D à l'aide de ce logiciel qui fonctionne sur le meme principe que les fractales.

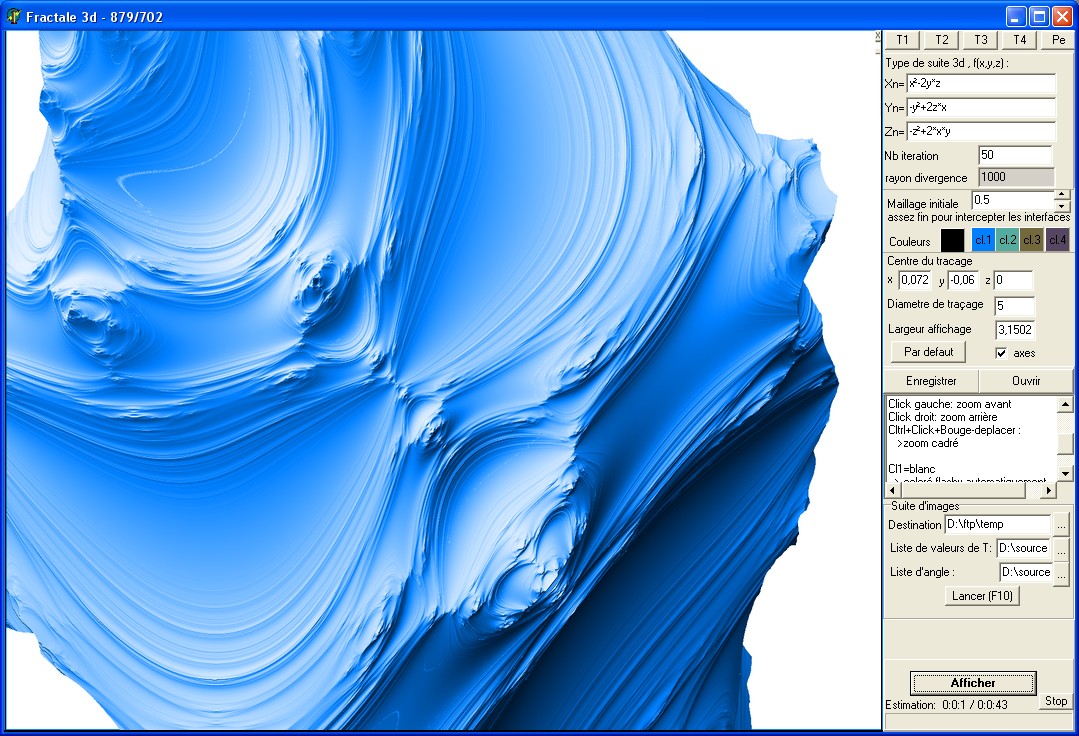
Nom du logiciel : Fractale 3D
Version : 1.0
Environnement : de Windows 95 à win10  (Sous Mac O.S., voir avec un émulateur windows)
Taille : 707 Ko
Langue : Français
Année de lancement : 2013-2024
Editions : Mike°Soft (C)
Licence : Usage gratuit
Logiciel ayant trait aux thèmes : Math -  Fonctions -  Graphisme -  Graphisme_conception -  Complexité -  Chaos

Généralités

On rentre un choix de formules de suites ou X, Y, Z s'expriment en fonction de ces 3 variables.
On pourra réaliser des figures 3D de formes très variables.
Le choix des couleurs donne plus ou moins de relief à la figure. (Deux couleurs qui se suivent, stoppent l'ajout des autres couleurs)

On pourra enregistrer et réouvrir une figure réalisée.

Manipulation du graphe

On peut tourner le graphe pour le voir sous tous les angles : avec la souris au centre pour 2 axes et sur les bords pour le 3eme axe.
Le diamètre de tracé et d'affichage, et le centre de tracage permette d'ajuster l'image à l'écran.

Création de film d'animation

Il est possible et intéressant de fabriquer des animations de ces objets 3D en agissant sur l'angle de vue et sur un paramètre T que l'on peut ajouter aux formules. Pour cela on constituera deux fichiers
- Un fichier txt contenant les valeurs de T .

Par exemple :
0
0,0001
0,0002
0,0003
0,0004
0,0005
0,0006
0,0007
0,0008
0,0009
0,001
etc...
Les valeurs seront lues et stopperont la fabrication une fois parvenu à la fin de la liste.

- Un fichier *.txt contenant les deux angles d'orientation lattitude longitude à chaque étape. Par exemple:
0/0
0,0314159265358979/0,0314159265358979
0,0628318530717959/0,0628318530717959
0,0942477796076938/0,0942477796076938
0,125663706143592/0,125663706143592
0,15707963267949/0,15707963267949
0,188495559215388/0,188495559215388
0,219911485751285/0,219911485751285
etc...
Les angles seront lus en boucle jusqu'à épuisement des valeurs de T (d'où l'intérêt de faire une boucle sans rupture qui pourra se répéter)
Le résultat est un ensemble d'images placées dans un répertoire que l'on peut compiler en un film à l'aide d'un logiciel de type 'image to video'.
Exemple d'animation

Méthode

Les fractales sont souvent réalisées à partir de suites dont on cherche la vitesse de divergence pour chaque pixel de l'écran.
Et bien, il s'agit à peu près de la même chose ici. Sauf qu'on le fait pour chaque point de l'espace et donc au lieu de fonctionner avec des suites de complexes (en 2 dimensions), les suites fonctionnent ici avec 3 dimensions Xn, Yn, Zn. Chaque point de l'espace et le "vecteur" intial de la suite qui se calcule par itérations (avec un maximum fixé) jusqu'à divergence (rayon de divergence fixé). La surface tracée est la suivante : pour chaque pixel de l'écran; on imagine une ligne droite partant de l'œil de l'utilisateur. Le premier point où a lieu un passage de divergence à non-divergence sera tracé (et sa couleur sera donnée par son inclinaison dans la forme globale par rapport à la lumière).

Dans les formules, on écrira avec x,y,z pour ne pas alourdir l'écriture, mais il faudra comprendre Xn, Yn, Zn,

Toutes les formules ne produisent pas des figures "interessantes". Pour obtenir une forme, quelques remarques sont utiles :
- avec une explosion des valeurs dès qu'une variable est grande (d'où la compacité de l'image). On peut donc choisir des polynomes de degré supérieur à 2.
- qu'il y ait les valeurs qui se compensent l'une l'autre pour produire des formes intéressantes. Par exemple des soustractions de dimensions similaires (exemple : x²-z*y)
-etc... à chacun sa réflexion et son imagination.

Le maillage initial est la distance intiale entre deux points successifs calculés, sur l'axe de l'œil. Un écartement long peut rendre inaperçu deux changement de divergence entre les deux valeurs. Un écartement court allonge beaucoup le temps de calcul... mais c'est nécessaire si l'on veut rendre tout ce qui est fin en épaisseur dans la figure , en particulier des bords de la figures.