Etude du Code Secret de la Bible - Analyse détaillée
III - MESURER LE SECRET
Le Code Secret, comme nous l'avons vu, repose sur un procédé mécanique ; cela présente l'avantage de pouvoir être mesuré par les Mathématiques. Beaucoup d'événements de la vie sont ponctuels et uniques ; dans ce cas il est impossible d'en donner une idée mathématique. Par contre dans le cas du Code Secret, les découvertes sont régies par un mécanisme précis et renouvelable, c'est pourquoi il est possible de mesurer mathématiquement les résultats qu'on obtient.
Il faut tout de même mettre un frein à la confiance absolue dans les chiffres. Les mathématiques, bien qu'elles soient une "science exacte", ne sont exactes que lorsqu'elles parlent d'elles-mêmes, lorsqu'elles restent cantonnées dans la théorie. Mais dès que les mathématiques viennent modéliser la réalité, elles ne sont plus aussi dignes de confiance, car pour établir une simulation il faut construire un modèle qui est toujours un peu différent de la réalité.
Construire un modèle conduit pratiquement toujours à des approximations, des simplifications ; tout simplement parce que la réalité est très complexe dans la plupart des cas. Mais au milieu de la complexité, il y a de nombreux détails qui sont souvent négligeables. Il est souvent inutile de s'y arrêter. Prenons un exemple courant : quand on jette un dé sur un sol plat, on ne se demande pas si le dé peut rester en équilibre sur une arrête ; c'est pourquoi on néglige cette possibilité, mais cela n'est pas une impossibilité certaine. Le modèle mathématique qu'on construit habituellement sur cet exemple dit qu'il y a une chance sur six de tomber sur chaque face, on ne compte pas les autres situations possibles. Heureusement cette approximation est plutôt précise et très proche de la réalité. Pourtant le modèle est simplifié, il est inexact au sens absolu des éventualités possibles. Lorsque un modèle mathématique est posé, le raisonnement et les calculs qui suivent sont toujours exacts si le mathématicien ne fait pas d'erreur. Par contre, il est impossible d'affirmer qu'un modèle colle parfaitement à la réalité. Si le modèle est établit objectivement on pourra tout de même affirmer que l'approximation est très précise. IL ne faudra donc pas s'étonner si l'on procède à quelques simplification qui rende les calculs plus simple sans dénaturer les résultats.
Que faut-il penser de ces remarques ? Il faut simplement toujours être prudent, même avec des mathématiques ; et nous aurons l'occasion de voir pourquoi. Par contre lorsqu'un modèle mathématique est établi et qu'il concorde bien avec la réalité, les résultats sont très fiables. La preuve est qu'on parvient à envoyer des fusées sur la Lune malgré la complexité des phénomènes à prendre en compte.
Il nous reste maintenant à établir le modèle mathématique du Code Secret. Ensuite nous donnerons les résultats issus de ce modèle.
Le modèle mathématique
Chaque titre de chapitre est suivi d'une note sur la difficulté des mathématiques qui y sont contenues. Le lecteur pourra utiliser ces renseignements pour conduire sa lecture.
Le choix du modèle est très important
Difficulté mathématique simple
Nous avons expliqué, et c'est fondamental, que pour calculer un événement, il faut poser un modèle. Voici un exemple : pour aller de Paris à Marseille, il y a 780 km ; en roulant à une moyenne de 120 km/h, il faut 6 heures et demi. Pour établir ce résultat, nous avons fait l'estimation suivante : notre véhicule roulera à 120 km/h. Mais ceci n'est véritablement qu'une estimation théorique. Il est peu probable que notre vitesse puisse constamment être de 120 km/h. Il y a d'un côté le modèle, de l'autre la réalité. On perçoit facilement ce que signifie un tel calcul et chacun saura bien comprendre les écarts entre ce modèle et la réalité. Il en est de même pour les estimations que nous allons établir. Il faut bien comprendre qu'elles apportent un résultat approchant la réalité, mais qui n'est pas significatif de l'exacte réalité qui est inaccessible.
Les choses se compliquent un peu lorsqu'il y a plusieurs façons de poser un modèle mathématique. Lorsqu'un problème n'est pas simple, on peut fréquemment apporter plusieurs explications différentes pour le comprendre. Et bien souvent les différentes approches donnent des résultats dissemblables. En voici un exemple : on lance au hasard, sur une petite table de billard de 1m², une boule de 5cm de diamètre. Supposons qu'on ait tracé une croix au centre de la table, on se pose la question suivante : "Quelle est la probabilité que la boule s'arrête sur la croix ?". Même en supposant que la boule soit vraiment lancée au hasard et qu'elle ait la même chance d'arriver partout sur la table, on peut malgré tout obtenir des résultats complètement différents. Tout dépend de ce qu'on appelle "arriver sur la croix". Si l'on entend par là que l'aplomb du centre de la boule doit être à moins de 0.5mm du centre de la croix - c'est-à-dire très précisément sur la croix - la probabilité est de 1 chance sur 1 273 239. Alors que si l'on accepte que la boule soit à moins de 2.5cm - c'est-à-dire qu'elle soit au-dessus du centre de la croix - alors la probabilité est de 1 chance sur 509. On s'aperçoit de l'énorme différence entre les deux compréhensions du phénomène. Il est fondamental de comprendre cela pour bien interpréter les probabilités. Il faut au départ poser le bon modèle, c'est-à-dire le modèle qui est psychologiquement le plus juste. Quel que soit le choix, il est toujours contestable ; il n'y a pas de modèle absolu. Le rôle du mathématicien est d'être le plus honnête possible pour poser un modèle réaliste. Dans le cas précédent, qu'auriez-vous choisi pour transcrire mathématiquement "arriver sur la croix" ? Est-ce arriver exactement dessus ? C'est mathématiquement impossible en théorie, il est nécessaire d'accepter un seuil de tolérance. Est-ce arriver très près alors ? Dans ce cas, jusqu'à quelle proximité accepte-t-on ? Ce sont des questions importantes, car 1 chance sur 500 et une chance sur 1 million ce n'est pas tout à fait semblable. Il faut donc être très lucide en posant un modèle. Il faut toujours bien comprendre ce que le modèle implique, c'est cela la lucidité indispensable à l'établissement d'un modèle objectif.
L'exemple de la boule, qui est d'un énoncé très simple, pose un problème important de choix du modèle. Heureusement nous n'aurons pas de dilemme aussi compliqué à trancher. Dans l'exemple précédent le problème est compliqué parce qu'on a affaire à des mesures continues (les mesures peuvent prendre toutes les valeurs) ; ce qui n'a pas lieu lorsqu'on ne fait que compter des objets (les résultats ne peuvent être que des valeurs entières). Et mesurer le Code Secret consiste avant tout à compter des objets, comme nous le verrons. Le choix du modèle sera donc moins difficile. Par contre, il restera d'autres questions à trancher.
Avant de commencer le travail fixons bien notre objectif : notre but est de parvenir à estimer les chances de découverte de chacun des tableaux présentés dans "La Bible : le Code Secret".
Probabilité ou Espérance ?
Difficulté mathématique assez simple
La première difficulté est de choisir si l'on va exprimer les résultats en probabilité ou en espérance mathématique. Pour vous ça n'a peut-être aucune importance, étant donné que vous n'en connaissez pas la différence. Comme nous l'avons vu, il est très important de bien comprendre de quoi nous parlons pour pouvoir apprécier les résultats.
Quelle est donc la différence entre une probabilité et une espérance ? Tout d'abord une probabilité est un nombre entre 0 et 1 (à moins que ce ne soit en pourcentage entre 0% et 100%), une probabilité exprime QUAND est-ce qu'une chose arrive. Alors que l'espérance est un nombre positif quelconque, il signifie COMBIEN de fois un événement se produit. Nous allons très vite voir la différence par un cas concret :
Imaginons une Faculté qui possède 10 amphithéâtres. Ils sont tous vides sauf un qui contient 200 personnes.
· Intéressons-nous premièrement à l'espérance : quelle est l'espérance de trouver des gens dans les amphithéâtres ? Cela signifie combien vais-je trouver de personne. Il y a 200 personnes, pour 10 amphithéâtres, l'espérance de trouver des gens est de 20 personnes. C'est la moyenne du nombre de gens que l'on trouve par amphithéâtre.
· Intéressons-nous maintenant à la probabilité : quelle est la probabilité de trouver des gens dans les amphithéâtres ? Cela signifie quand est-ce que je vais trouver quelqu'un ? Et bien, il arrivera que je trouve quelqu'un dans un cas sur 10. La probabilité est de 0.1 (10% de chance).
L'exemple est choisi pour montrer que la différence de résultats entre probabilité et espérance peut être très contrastée. On s'aperçoit en outre que l'utilisation de la probabilité perd des informations : en particulier si le nombre de gens avait été de 3 au lieu de 200, le résultat aurait été le même ; la probabilité ne tient pas compte du nombre, elle tient compte de quand a lieu un événement. L'espérance à l'opposé ne dit pas comment sont répartis les gens dans les amphithéâtres, elle donne seulement une moyenne.
Maintenant que nous avons une petite notion de ce que sont l'espérance et la probabilité, essayons d'aborder un problème un plus proche de notre besoin. L'objet de notre étude est de savoir si un mot choisi peut ou non apparaître dans la Bible par le procédé du saut de lettres. Prenons un exemple simple : observons l'apparition d'une seule lettre. Supposons que nous ayons un livre de 170 pages et que nous voulions y trouver la lettre 'y'. On se pose la question suivante : En ouvrant le livre au hasard, quelle est la chance de trouver la lettre 'y' dans la page ouverte ? La question paraît simple, pourtant il y a plusieurs façons de se poser cette question :
· On peut premièrement se demander quelle est la chance de trouver la lettre 'y' dans la page ouverte ? C'est à dire quel est la chance qu'il y ait au moins un 'y', peu importe le nombre. Cette question correspond à la probabilité ; on désire savoir quand est-ce qu'il y a des 'y'. Pour obtenir ce résultat, il suffit de compter les pages qui n'ont pas de 'y'. Supposons qu'en comptant, nous trouvions 12 pages sans 'y', soit 7 % du livre. La probabilité qui répond à notre question est donc 0.93 ; c'est-à-dire qu'on a 93 chances sur 100 de trouver au moins une fois la lettre 'y'.
· On peut aussi s'intéresser à la question suivante : combien de fois peut-on trouver la lettre 'y' dans une page ouverte au hasard ? En comptant méthodiquement, on s'aperçoit qu'il y a 400 fois la lettre 'y' dans tout le roman. La réponse à notre question est donc simple : on risque de trouver la lettre 'y' 2,35 fois par page en moyenne. L'espérance qui répond à notre question est 2, 35
.
Dans le premier cas, nous avons vu la probabilité de trouver la lettre 'y' ; dans le second, nous avons calculer l'espérance de trouver la lettre 'y'. La différence entre ces deux mesures est claire et précise.
Il nous faut trancher pour savoir quelle mesure utiliser : l'espérance ou la probabilité. Pour choisir, revenons en à notre problème de départ : nous désirons estimer s'il est possible de faire apparaître un mot dans la Bible en sautant des lettres. Or il y a plusieurs façons d'exprimer cette question ; parmi les deux qui suivent laquelle vous paraît la plus intéressante ?
Supposons que nous ayons choisi de rechercher un mot précis à l'intérieur d'un livre.
- Peut-on trouver ce mot dans le livre ?
- Combien de fois peut-on trouver ce mot dans le livre ?
Je crois que la deuxième question est plus intéressante pour nous, car elle nous permet non seulement de connaître si nous pouvons trouver le mot, mais aussi combien de fois nous risquons de le trouver. C'est pourquoi nous exprimerons nos résultats uniquement avec des espérances et non des probabilités qui perdent une partie des résultats.
Il y a une raison supplémentaire à ce choix, c'est que l'espérance se calcule beaucoup plus simplement que les probabilités. Elle sera donc plus facile à comprendre.
Comment faut-il comprendre les résultats ?
En moyenne...
Difficulté mathématique assez simple
Il faudra faire attention en lisant les résultats pour ne pas se méprendre sur ce qu'ils signifient. Lorsqu'on obtiendra une espérance de 3.5, cela signifiera qu'on risque de trouver le mot étudié 3.5 fois. Un résultat de 0.5 signifie qu'on risque de trouver le mot une demi-fois. Mais comment cela est-il possible ? Il faut faire attention : une espérance de 0.5 ne veut pas dire qu'on trouvera le mot cherché une fois sur deux lorsqu'on essaierait de nombreuse fois, mais qu'on trouve le mot une fois sur deux en moyenne. Ce n'est pas la même chose, ce résultat nous dit combien de fois, on peut trouver le mot : une fois sur 2, mais il ne nous dit pas quand on risque de le trouver.
Il ne faut pas confondre les résultats d'une espérance et d'une probabilité, car ils n'ont pas le même sens. Si une probabilité est de 1 (c'est-à-dire 100 %) cela signifie qu'on est sûr de trouver ce qu'on cherche. Mais si une espérance est de 1, il faut faire attention ; cela ne signifie pas qu'on trouvera forcément ce qu'on cherche à tous les coups, mais qu'on le trouve une fois en moyenne, par essai. Si l'espérance est de 1, il se peut que sur 100 essais, on ne trouve ce qu'on cherche que 85 fois (la probabilité serait de 0.85) ; mais dans ce cas il y a forcément dans ces 85 essais, des essais où l'on a trouvé le résultat plusieurs fois, soit deux fois, soit trois fois, etc._ en tout il y a eu 100 résultats positifs.
Lorsque l'espérance est supérieure à 1, il en est de même. Une espérance de 8 signifie qu'on peut espérer voir apparaître ce qu'on cherche 8 fois ; ce résultat est une moyenne sur l'ensemble de tout ce qu'on pourrait essayer.
Faisons une dernière remarque : il arrivera souvent que nous utilisions un abus de langage dont il faut être bien conscient. Lorsqu'on trouve une espérance de 0.2, cela signifie qu'on risque de trouver le résultat recherché 0.2 fois en moyenne sur l'ensemble des recherches, cela signifie qu'en moyenne nous trouverons le résultat une fois sur 5 essais. Cela ne signifie pas que l'on va voir se produire l'événement attendu une fois sur cinq, mais que ses apparitions se font en moyenne une fois sur 5 (pour comprendre cette différence, revenons à un exemple précédent : l'espérance nous disait qu'il y avait 20 personnes par amphithéâtre en moyenne. Ce n'était pourtant pas le cas réel, c'était une moyenne, car les 200 personnes étaient toutes dans le même amphithéâtre) . C'est pourquoi, en parlant d'espérance, lorsqu'on dit : "il y a une chance sur 5 de voir arriver l'événement", il faut bien comprendre que l'on parle de combien et non pas de quand. Une chance sur 5 ne signifie pas une fois sur 5 en constatation , mais une fois sur 5 en moyenne d'apparition. C'est pourquoi en utilisant cette formulation un peu trompeuse, nous ajouterons les mots "en moyenne", afin de bien se rappeler qu'il faut comprendre les résultats en nombre d'apparitions et non pas en moment d'apparition.
De même, lorsque l'espérance de trouver un mot sera de 1 sur 5, il nous arrivera abusivement de dire : "il suffit de faire 5 essais pour espérer trouver le mot", il faudrait ajouter à la fin de cette phrase , "...une fois en moyenne". Car une espérance de 1 sur 5 ne nous dit pas que le résultat arrivera une fois sur cinq essais, mais que la moyenne du nombre des résultats équivaut à ce que le mot apparaisse une fois sur 5, ce qui n'est peut-être pas le cas.
Maintenant, il faut tout de même nuancer un peu cette différence entre probabilité et espérance: par exemple lorsqu'un calcul, nous donnera une faible espérance comme 1 sur 100, il arrivera en général que le mot ayant cet espérance apparaissent aussi une fois sur 100 en pourcentage d'essais (cela signifie qu'un mot ayant une espérance de 1 sur 100 possède aussi une probabilité de 1 sur 100, ou très légèrement moins). En effet, on pourrait montrer que dans les exemples que nous rechercherons, lorsque l'espérance est faible, elle possède une valeur très proche de la probabilité. Cela vient du fait que les événements que nous allons étudier sont, en général, uniformément répartis, c'est à dire que les résultats ne sont pas concentré sur certains essais (pour reprendre l'exemple du départ, on ne trouverait jamais 200 élèves dans un amphithéâtre, et aucun ailleurs). Cette constatation permet donc d'atténuer la gravité du contresens qui est fait lorsqu'on interprète une espérance de 0.1 en disant que l'événement arrive une fois sur 10. Pour résumer cette dernière idée, disons que la confusion entre espérance et probabilité n'est pas très dommageable quand les résultats sont faibles.
Au pire...
Il convient aussi de bien expliquer un autre principe important dans le calcul des espérances. Imaginons l'expérience suivante : on bande les yeux d'un homme qu'on fait entrer dans une pièce ronde ; on lui annonce que sur le mur de 9 mètres de circonférence se trouve tracé un trait vertical que l'homme ne voit pas. L'expérience consiste à donner une épingle à cet homme afin qu'il la plante dans le mur, en espérant qu'il se rapproche au maximum du trait. Supposons maintenant qu'un essai donne le résultat suivant : un candidat a planté l'épingle à 3,75 cm du trait. C'est un résultat remarquable : en supposant que l'homme puisse planter l'épingle n'importe où dans le mur de façon indifférente, un pareil résultat ne se produit qu'une fois sur 120 ( en effet 900cm / ( 3.75cm x 2 ) = 120, le coefficient 2 vient du fait qu'il peut être d'un coté ou de l'autre du trait). Un résultat ayant une valeur de 1 chance sur 120 est assez remarquable.
Soyons plus précis : l'épingle a été planté à 3.75 cm du trait, le fait de planter au hasard une épingle à la distance exacte de 3.75cm est un événement pratiquement impossible. Car si l'on mesure la distance avec une grande précision, il y a très peu de chance de planter l'épingle exactement à cet endroit : à 3.75 cm du trait ; il en est de même d'ailleurs pour toutes les autres positions. N'importe laquelle des positions où l'on peut planter l'épingle est pratiquement impossible. Cela provient du fait que les positions éventuelles sont innombrables (presque infinies en théorie). Ainsi chacune d'elle est presque impossible. La question subséquente est donc : comment mesurer la probabilité que l'aiguille arrive à 3.75 cm, si cette probabilité est pour ainsi dire nulle ?
Si l'on revient maintenant à l'expérience, ce qui nous intéresse ce n'est pas que l'épingle soit exactement à 3.75 cm du trait, mais qu'elle soit le plus proche possible du trait. Pour mesurer le fait que l'aiguille soit plantée à 3.75 cm du trait, on ne mesurera pas la probabilité de tomber exactement à 3.75 cm, mais la probabilité de tomber au maximum à 3.75 cm, c'est-à-dire la probabilité que l'aiguille tombe AU PIRE à 3.75cm. La mesure ainsi obtenue correspond bien à l'impression psychologique : "planter l'aiguille assez près du trait" (à une proximité de 3.75 cm).
C'est un principe constant dans toutes les mesures de probabilités ayant rapport aux phénomènes continus. On ne mesure la probabilité qu'un événement arrive exactement comme on l'a vu se produire, mais la probabilité qu'il arrive au pire comme on l'a vu se produire. Si l'on s'arrête un peu sur ce principe, on s'aperçoit que c'est la meilleure, sinon la seule façon de procéder. Il faut être conscient de ce principe pour bien interpréter des résultats.
C'est ce principe de mesure que nous allons utiliser pour énoncer les résultats que nous chercherons. En particulier lorsque nous chercherons à mesurer l'apparition de plusieurs mots se croisant dans un même tableau. Nous ne donnerons pas l'espérance de trouver exactement les mots considérés à la place qu'ils occupent, mais plutôt l'espérance de trouver un résultat qui ait au pire une impression psychologique similaire. Ceci donnera la mesure du tableau.
Si pour un tableau particulier nous trouvons une espérance de 15, cela signifiera qu'on peut trouver en moyenne au moins 15 tableaux similaires OU MIEUX ENCORE. Voilà le sens précis qu'il faudra donner aux résultats que nous trouverons.
Plan de recherche
Avant de rentrer dans le vif du sujet, prenons le temps de fixer quelle sera notre démarche, afin de toujours garder un fil conducteur pour toutes les explications et démonstrations que nous allons effectuer. Ce plan permettra au milieu d'un dédale d'explications de se souvenir du but à atteindre.
Essayons de comprendre quel est le but de notre recherche : nous désirons pouvoir mesurer si les tableaux du livre de Drosnin sont le résultat naturel du hasard, ou si leur présence est mathématiquement inexplicable. Nous avons vu que pour établir ces résultats il faut mesurer chaque tableau au moyen des Espérances Mathématiques. Les résultats obtenus nous permettrons de savoir si les tableaux sont issus d'un mécanisme naturel ou non, suivant que les espérances trouvées sont assez élevées, ou bien très faibles. Il nous reste donc à savoir comment calculer l'espérance d'un tableau. C'est le but de toute notre recherche.
Le modèle mathématique qui permet d'évaluer les tableaux doit être calqué sur le mécanisme utilisé pour construire ces tableaux. Or nous avons vu que la méthode la plus simple pour faire apparaître des mots qui se croisent est de rechercher premièrement le mot principal. Lorsque celui-ci - (ou ceux-ci lorsqu'on trouve plusieurs mots principaux possibles) - est découvert, il faut alors rechercher si l'on peut trouver le premier mot satellite à la périphérie du mot principal. Lorsque le premier mot satellite est découvert, on peut ensuite chercher si l'on trouve d'autres mots satellites, à proximité des deux premiers.
1. C'est ainsi que nous cherchons d'abord à déterminer l'espérance d'un mot principal (ou d'un mot seul, ce qui revient au même). C'est la première partie de notre recherche traiter dans le paragraphe : "Mesurer la découverte d'un mot".
2. Ensuite nous chercherons à déterminer l'espérance de découvrir un premier mot satellite à proximité d'un mot principal qui a déjà été trouvé. Cela sera traité dans la partie : "Mesurer la découverte du deuxième mot".
3. Lorsqu'on a mis en évidence deux mots qui se croisent, on peut chercher à faire apparaître un troisième mot, un quatrième mot, etc_ Nous aborderons cela dans la partie intitulée : "Mesurer la découverte des mots suivants".
Le premier point est le plus facile à traiter, le second est probablement le plus difficile et la troisième partie suit assez logiquement la deuxième partie.
Le modèle que nous allons construire est loin d'être le seul qui puisse mesurer les tableaux. Par contre selon le procédé de recherche que nous avons établi, qui consiste à chercher les mots les uns après les autres, le modèle sera parfaitement adapté et permettra de mesurer réellement les tableaux construits selon cette chronologie.
Nous avons bien précisé que le modèle doit se calquer sur la méthode avec laquelle on recherche les tableaux, mais si les tableaux ont été découverts par une autre méthode, est-ce que le modèle convient encore ? En particulier, les exemples de tableaux que nous avons conçus dans les chapitres précédents n'ont pas été construits selon la méthode que nous expliquons qui consiste à rechercher le mot principal, puis les mots satellite, etc... Tous les tableaux que nous avons découverts dans le livre de Pascal, ou dans le livre fait de lettres tirées au hasard sont le fruit d'un programme informatique qui utilise une méthode plus performante. La méthode consiste à analyser toutes les positions de chacun des mots recherchés et produire les meilleurs tableaux où ceux-ci se croisent.
Notre modèle est-il alors inadapté pour mesurer des tableaux qui n'ont pas été construits selon la logique chronologique du modèle que nous exposons ? La réponse est évidemment négative, notre modèle pourra mesurer tous les tableaux ; seulement, les espérances obtenues se rapporteront à la méthode de recherche chronologique (recherche du mot principal d'abord, puis premier mot satellite ensuite, etc...). En effet, il est possible de rechercher n'importe quel tableau par cette méthode chronologique, il est donc aussi possible de mesurer tous les tableaux avec le modèle que nous allons construire. Il faut remarquer par ailleurs qu'il est possible que les espérances que nous trouvions par notre modèle soient sous-évaluées. Cela provient du fait qu'en disposant d'une méthode de recherche plus efficace, on augmente les chances de découverte.
Si les résultats sous-évalués sont une preuve - et nous verrons qu'ils le sont - à combien plus forte raison des résultats plus précis le seraient aussi. En fait, on peut s'apercevoir qu'en choisissant une méthode ou bien une autre, la différence des résultats n'est pas flagrante. Il convient donc d'essayer de construire un modèle qui privilégie la simplicité. Malheureusement la simplicité reste toujours bien relative_
Mesurer la découverte d'un mot
Nous voilà fixés sur la façon de présenter les résultats et sur la façon dont il faut les comprendre. Il nous reste à faire le plus difficile maintenant, c'est fixer le modèle.
Modèle de base
Difficulté mathématique simple
Nous allons d'abord construire un modèle simplifié afin de comprendre comment fonctionne les calculs ; ensuite nous poserons un modèle plus réaliste qui donne des résultats plus précis.
Posons clairement le problème : notre but est de déterminer l'espérance d'apparition d'un mot quelconque dans la Bible. Il serait par exemple intéressant de trouver si notre nom se trouve dans la Bible. Choisissons un mot pour fixer les idées, le mot 'code'. Ce mot existe-t-il ? Est-il caché par le Code Secret dans le texte biblique ? Il faut le décoder. Il faut trouver si, en sautant des lettres, il est possible de le faire apparaître. Ce mot existe-t-il ? Et s'il existe, combien de fois peut-on le trouver dans la Bible ? Il est entièrement possible de prévoir cela mathématiquement, c'est ce que nous allons découvrir. On pourrait utiliser un ordinateur pour voir si le mot s'y trouve ; un ordinateur assez puissant de préférence, car cette recherche risque d'être assez longue. Seulement cela ne nous dit toujours pas si ce que nous trouvons est normal ou non. C'est pourquoi il est encore plus intéressant de prévoir le résultat mathématiquement.
Avant de travailler sur la Bible, nous allons travailler sur un autre texte afin de comprendre comment fonctionne cette recherche. Nous allons utiliser un texte avec des lettres françaises, c'est plus facile à comprendre. Supposons de plus que le texte ne signifie absolument rien. C'est un ordinateur qui aurait tiré des lettres au hasard sans aucun sens, sans même aucun espace entre les lettres. Quelque chose de ce genre :
"onoeemsleneemntrrdosuutclgeiuuraainenennmuueenumrdosstomepereanreeoeuesuelrnblhseunoiouaieeilveileqeovtetmaiiodeeouiieoaueosmdpclooeuuuadecucevaclrtnfaeseeimsdsasssdeurenepecooeluttsuuisblataeeutaietetvoeaaeccvfandutaeirledeeutthhobdlopesslreaaetlmnonudsucandnrnnanhescevartpsesrrisssseuinetuoimiemaicpaerlletticlimqaitmeeeemotrmseuetdleruvlnkmaeaessllninsetdostenpoiluedeeumipaesultsiaiitatilseulltleeadeiettesaeieeoselidneseurimsvslebsanegeeqeletuumefdneaoscaasettuuessedsastvmreantoaerdliosctsaitetemnrolutpeoolanrrurqscuoansrelmieltuhenjdiusuuscpsdnrereaelnossmrerumelcuceeeuuceuepcsjuvoozoiluetoatutnoemeioag"
Mais au lieu de quelques lignes, nous supposerons que nous disposons de tout un livre de 305 000 lettres, car c'est à peu près ce nombre de lettres que contient le texte de la Bible utilisée pour les recherches du Code Secret. Ce serait un livre pas vraiment intéressant en soi_ Par contre, il va nous être bien utile pour comprendre ce que nous désirons connaître.
Pour une seule lettre
Difficulté mathématique simple
Nous allons simplement commencer par chercher si nous pouvons trouver dans notre fameux livre la première lettre du mot 'code', la lettre 'c'. Quelle est l'espérance de trouver cette lettre 'c' dans le texte ? Ce calcul est très simple. Etant donné qu'il y a vingt six lettres dans l'alphabet français et qu'on a supposé le texte composé de lettres au hasard, alors la lettre 'c' sort une fois sur 26 en moyenne. Comme il y a 305 000 lettres, cela fait une espérance de lettres. Cela ne veut pas dire qu'il y a forcément 11 731 lettres 'c' dans le texte. D'ailleurs en comptant le nombre de 'c' dans des milliers de livres différents fabriqués avec 305 000 lettres au hasard, il y aurait extrêmement peu de livre où l'on trouverait exactement 11 731 fois la lettre 'c'. Par contre, on s'apercevrait que la plupart des fois le nombre de lettre 'c' est assez proche de 11 731. On s'apercevrait même d'une chose plutôt surprenante : En faisant la moyenne des résultats trouvés, on obtiendrait exactement 11 731 (si on a compté sur un assez grand nombre de livre). C'est un résultat que les mathématiques peuvent prévoir.
Ceci est un résultat très important qui est à la base de tous les calculs que nous allons faire. On pourrait exprimer ce résultat à peu près ainsi : lorsqu'on répète un très grand nombre de fois une expérience, la moyenne des résultats s'approche de plus en plus de l'estimation calculée (si la modélisation a été bien faite). Pour preuve, nous vous proposons de faire l'expérience suivante : lançons un dé un très grand nombre de fois, et intéressons-nous aux valeurs obtenues par le dé : les valeurs qui peuvent apparaître sont le 1, le 2, etc_ jusqu'à 6. L'expérience consiste calculer la moyenne de tous les résultats obtenus. Par exemple si en jetant le dé 14 fois nous obtenons les résultat suivants : 3, 4, 6, 1, 2, 2, 5, 3, 4, 5, 1, 3, 2, 4, nous dirons que la valeur moyenne des résultats est de (3+4+6+1+2+2+5+3+4+5+1+3+2+4)/6=3.21. Quel est l'intérêt de cette expérience ? C'est de montrer que le mathématique permettent de prévoir exactement la moyenne lorsque le nombre de lancers de dé est suffisamment grand. En effet, que si nous réitérons un grand nombre de lancer de dé, nous pouvons affirmer que nous trouverons une moyenne proche de 3.5. En voici la raison : chaque numéro de 1 à 6 sur le dé à la même chance d'apparaître qui est de 1 chance sur 6. Ainsi, sur un très grand nombre de lancers, chacun des chiffres de 1 à 6 apparaîtra un nombre de fois à peu près identique par exemple chacun environs 150 fois. On peut obtenir par exemple 145 fois le 1, 154 fois le 2, 138 fois le 3, 161 fois le 4, 152 fois le 5 et 149 fois le 6. La moyenne des points obtenus sera donc (145x1+154x2+138x3+161x4+152x5+149x6)/(145+154+138+161+152+149)=3.52. Lorsqu'on joue un très grand nombre de fois le dé, les différentes faces apparaissent un nombre de fois à peu près égales. Si on considérait qu'en jouant un très grand nombre de fois le dé, les faces apparaissaient un nombre de fois exactement égales, on pourrait simplifier le calcul de la moyenne en calculant directement la moyenne des valeurs du dé ; c'est-à-dire par le calcul suivant : (1+2+3+4+5+6)/6=3.5 . C'est exactement le résultat vers le quel tend la moyenne lorsqu'on joue indéfiniment. Il faudra être patient, car pour être sûr d'obtenir ce résultat, il faudrait lancer le dé un nombre de fois très important. Et plus on veut un résultat proche de 3.5, plus il faudra lancer le dé un grand nombre de fois. En théorie, en jouant sans s'arrêter, on pourrait aller aussi près qu'on veut de 3.5 si l'on est assez patient (et si les dés sont parfaitement équilibrés).
L'intérêt de cette expérience permet de montrer que lorsqu'on peut produire une expérience un grand nombre de fois, les mathématiques peuvent très souvent prévoir le résultat moyen de ces expérience. C'est exactement le type de problème auquel on a affaire avec le Code secret.
Pour plusieurs lettres
Difficulté mathématique assez simple
Nous avons étudié la lettre 'c'. Maintenant nous allons renouveler la même étude pour tout le mot 'code'. Combien de fois peut-on espérer le trouver dans notre fameux livre ? Souvenons-nous que ce livre est fabriqué de lettres au hasard. Il se pourrait par exemple qu'on trouve le mot 'code' au tout début, dans les quatre premières lettres du livre. Comme les lettres sont tirées au hasard et qu'il y en 26, l'espérance de trouver la lettre 'c' en première position est de 1/26. Mais l'espérance de trouver la lettre 'o' exactement en deuxième position est aussi de 1/26, car les 26 lettres ont la même espérance d'être à cette deuxième position, comme à n'importe quelles positions d'ailleurs. A chaque position on peut trouver n'importe quelle lettre.
La question qui suit est de savoir quelle est l'espérance de trouver la lettre 'c' en première position en même temps que la lettre 'o' en deuxième position. Pour comprendre cela, il faut voir qu'il y a 1 chance sur 26 d'avoir le 'c' en première position ; c'est-à-dire que sur 26 livres différents, il y en a un seul en moyenne où le 'c' est en première position ; Ou encore, sur 676 (= 26 x 26) livres il y en a 26. Puis il faut le 'o' en seconde position, c'est-à-dire à nouveau une chance sur 26. Sur les 676 cas au départ, il n'y en a que 26 où la lettre 'c' est en première position. Sur ces 26 livres, il n'y en a qu'un qui ait le 'o' en deuxième position. Il y a donc un seul livre en moyenne sur les 676 où les deux premières lettres sont 'co'. On constate que l'espérance d'avoir les deux lettres au début est tout simplement le produit des espérances de chaque lettre. On obtient le résultat par le calcul suivant (1/26 x 1/26 = 1/676).
Ce résultat se généralise en une loi mathématique : si l'on veut obtenir en même temps deux résultats indépendants (c'est-à-dire qui ne se gênent pas l'un et l'autre en quelque sorte), il suffit de multiplier les espérances de chacun d'eux pour obtenir l'espérance des deux réunis.
Par ce principe, on obtient facilement l'espérance d'obtenir le mot 'code' dans les quatre premières lettres du livre : (1/26 x 1/26 x 1/26 x 1/26 = 1/456976), c'est un résultat très faible, 1 chance sur 456976. Il faut comprendre que sur 456 976 livres fabriqués avec des lettres au hasard, nous risquons d'en trouver 1 seul dont les quatre premières lettres sont 'code'. Autant dire qu'il faudrait de la patience_ Ce nombre est si faible que nous pourrions nous demander s'il est même possible de trouver le mot 'code' dans la Bible, même le moyen du saut de lettres qui ne fait qu'augmenter un peu les chances,_ nous verrons.
Les positions possibles
Difficulté mathématique un peu plus élevée
Notre problème n'est pas encore résolu. Notre question était : combien de fois peut-on espérer trouver le mot 'code', non pas au début mais n'importe où dans le texte, même en sautant des lettres. Là encore les choses se corsent un petit peu plus. Nous allons décomposer le problème.
Pour une taille de saut déterminée
La première question qui va nous intéresser est de savoir à combien de positions différentes le mot 'code' peut apparaître. La réponse est : un bon paquet ! Pour les compter, il faut les rechercher méthodiquement.
Le mot peut apparaître en première position, comme nous l'avons vu. Il peut aussi apparaître en deuxième position, c'est-à-dire en commençant à la 2ème lettre du texte. Par exemple si le livre commençait par 'wcodekjhfhsdfjd_', on dirait que le mot 'code' apparaît en 2ème position. Ensuite, il peut apparaître à la 3ème, la 4ème, la 5ème position_ jusqu'à la 304 997ème position. En effet, la dernière position possible pour la lettre 'c' n'est pas dernière lettre du texte, car il y a encore trois lettres derrière. Regardons la fin d'un texte dans un exemple : '_qsdfjkljcode'. En sachant que le texte a 305 000 lettres, on s'aperçoit que le 'c' est à la 304 997ème position. On obtient un total de 304 997 positions possibles pour le mot 'code' écrit en lettres collées.
Maintenant si on prend une lettre toutes les deux lettres et qu'on voit apparaître le mot 'code' - c'est le cas par exemple dans le texte suivant : '_fdkhfpoickoedlemkffdij_'. - on dira que le mot 'code' apparaît avec un saut de 2 lettres. On peut se demander combien de fois le mot 'code' peut apparaître de cette façon dans 305 000 lettres. Pour un saut de 2 lettres, la lettre 'c' peut à nouveau être à la 1ère position, à la 2ème,à la 3ème, etc._ jusqu'à la 305 000 - 6 = 304 994ème position, car 6 est la place nécessaire pour que le mot code puisse apparaître avec un saut de 2 lettres. Ceci fait à nouveau 304 994 positions possibles pour le mot 'code'.
Il y encore les cas où le mot apparaîtra avec un saut de 3 lettres, de 4 lettres, etc. Imaginons un saut de 600 lettres : combien de positions sont possibles ? La 1ère position est possible, la 2nde aussi, la 3ème également, etc_ jusqu'où ? Il faut commencer à compter précisément : le mot 'code' est fait de 4 lettres ; s'il apparaît dans le livre avec un saut de 600 lettres, cela veut dire qu'entre le 'c' et le 'o' il y a 599 autres lettres, de même entre le 'o' et le 'd' puis entre le 'd' et le 'e'. Le mot occupe une place totale de 1+599+1+599+1+599+1=1801 lettres. On peut donc trouver la dernière position possible pour le mot 'code' en saut de lettres 600. Cette dernière position est 305 000 - 1800 = 303 200. En effet il faut retirer 1800 à 305 000, et non pas 1801, car il ne faut pas retirer le 'c' puisque c'est lui qu'on essaie de placer.
Passons maintenant à une explication un petit peu plus compliquée. Au lieu de refaire les mêmes calculs pour chaque taille de saut différent, on va essayer de construire une formule. Pour cela on va utiliser des lettres à la place des chiffres. On va dire que le mot 'code' apparaît avec un saut de s lettres, (s comme saut). Le nombre de saut s, peut prend une valeur quelconque : 3, 5, 180 ou 15 384_ Cela n'a aucune importance. Ce chiffre, quel qu'il soit, sera noté par s.
Notre première question est : pour un saut de s lettres, quelle place occupe le mot 'code' dans le texte ? Entre le 'c' et le 'o', il y a s-1 autres lettres, de même entre le 'o' et le 'd' puis entre le 'd' et le 'e'. Le mot occupe une place totale de 1 + ( s-1 ) + 1 + ( s-1 ) + 1 + ( s-1 ) + 1 = 3 s + 1.
La seconde question est : combien de positions sont possibles pour le mot 'code' avec un saut de s lettres ? Selon le même raisonnement que précédemment 305 000 - 3s (car il ne faut pas ôter la première lettre 'c'). D'où vient le nombre 3 dans cette formule ? Le mot 'code' est fait de quatre lettres. Pour un mot de quatre lettres, il y a 3 intervalles entre les lettres : entre le 'c' et le 'o', entre le 'o' et le 'd', puis entre le 'd' et le 'e'. Le chiffre 3 est tout simplement le nombre de lettres moins une : 4 -1.
Pour un mot de 10 lettres, on pourrait refaire le même calcul. Pour qu'il apparaisse parmi les 305 000 lettres du texte avec un saut de s lettres, il y a 305 000 - 9s positions possibles.
On obtient finalement la formule suivante :
- pour un mot de m lettres,
- avec des sauts de s lettres,
- dans un texte de T lettres,
On obtient :
T - (m-1).s positions possibles.
Quelle taille de saut maximale ?
Nous savons calculer combien il existe de positions possibles pour chaque saut. Mais il reste une question importante : jusqu'à quelle taille de sauts peut-on aller ? Quelle est la taille du saut maximal ? Prenons comme exemple le mot 'mystérieux', il comprend 10 lettres. On peut chercher en tâtonnant : avec un saut de 33 889 lettres, le mot occupe une place de 33 889 x 9 + 1 = 305 002 lettres : c'est trop. Le plus grand saut possible est donc de 33 888 lettres. Mais comment trouver ce nombre de façon mécanique ? On a vu que, pour un saut de s lettres, le mot occupait une place de 9 x s + 1 lettres ; il suffit simplement que 9 x s + 1 £ 305 000, c'est-à-dire que 9 x s £ 305 000 -1 puis en divisant par 9 que s£(30500-1)/9, or (30500-1)/9= 33 888,7777... Donc s, qui est forcément un nombre entier, vaut au maximum 33 888 .
On peut généraliser ce calcul par le même raisonnement :
- pour un texte de T lettres,
- pour un mot de m lettres,
- pour un saut de s lettres,
La saut maximale est le plus grand nombre entier inférieur ou égal à (T-1)/(m-1), qui sera noté: Ent[(T-1)/(m-1)] avec Ent pour dire entier.
Nous avons construit les deux formules essentielles qui vont nous permettre de déterminer ce que nous cherchons. Qu'est-ce qu'on cherchait d'ailleurs ? Ah oui ! Le nombre total de positions possibles totales pour le mot 'code' dans un texte farfelu de 305 000 lettres.
Nombre total de positions
Nous savons déterminer pour chaque saut de s lettres combien il y a de positions possibles. Nous savons de plus que les sauts peuvent varier de 1 (pour des lettres collées) jusqu'à Ent[(T-1)/(m-1)]. Et bien il ne reste plus qu'à calculer la somme de ces positions possibles.
Si on a un texte de taille T, un mot de taille m, le nombre de positions possibles est donc :
[ T - (m-1).1 ] + [ T - (m-1).2 ] + [ T - (m-1).3 ] + . . .+ [ T - (m-1). ]
Il est possible de simplifier cette expression en utilisant une astuce mathématique. On pose l'opération en prenant deux fois cette somme, une fois à l'endroit et une fois à l'envers :
shapeType20fFlipH0fFlipV0lineColor13948116lineWidth0shadowOffsetX0shadowOffsetY-12700shadowOriginY32385fShadow1
[ T - (m-1).1 ] + [ T - (m-1).2 ] + . . .+ [ T - (m-1). ( Ent[(T-1)/(m-1)]-1) ] + [ T - (m-1).Ent[(T-1)/(m-1)] ] +
[ T - (m-1).Ent[(T-1)/(m-1)] ] + [ T - (m-1). (Ent[(T-1)/(m-1)] -1)] + . . .+ [ T - (m-1).2 ] + [ T - (m-1).1 ]
= [2.T - (m-1). (Ent[(T-1)/(m-1)] +1)] + [ 2.T - (m-1). (Ent[(T-1)/(m-1)] +1)] + . . .+ [2.T - (m-1). (Ent[(T-1)/(m-1)]+1)] + [ 2.T - (m-1).Ent[(T-1)/(m-1)] +1)]
Par cette astuce, en regroupant les sommes par deux, on trouve à chaque fois la même somme. On la trouve en tout Ent[(T-1)/(m-1)] fois. Ainsi la double somme est égale à :
= [ 2T - (m-1). (Ent[(T-1)/(m-1)]+1)] .Ent[(T-1)/(m-1)] , ce résultat vaut deux fois la somme totale qu'on cherche. Il suffit de diviser par 2. La somme qui nous intéresse est donc donnée par la formule suivante :
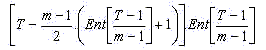
Ceci est le nombre de positions possibles pour un mot de longueur m dans un texte de longueur T constitué de lettres alignées au hasard et avec tous les sauts de lettre possibles permis.
Notre question était : à combien de positions différentes peut-on trouver le mot 'code' dans un texte de 305 000 lettres ? La réponse est donc:
![]()
Voici le résultat tant attendu. Nous naviguons dans les grands nombres. Pour avoir une idée plus précise de ce que signifie ce nombre : avec 15 500 000 000 oranges placées côte à côte, nous ferions plus de 27 fois le tour de la terre_ c'est donc un très grand nombre.
La réponse pour plusieurs lettres
Difficulté mathématique assez simple
Il est maintenant temps de répondre à la question initiale, celle qui nous intéressait en premier lieu : combien de fois peut-on espérer trouver le mot 'code' dans un texte hasardeux de 305 000 lettres ?
Nous avons vu que l'espérance de trouver le mot 'code' dans les 4 premières lettres était de 1 chance sur 456 976. Or si, au lieu de le trouver occupant les quatre premières lettres, on désirait le trouver en 4ème position avec un saut de 3 lettres (comme ici dans le texte suivant : 'ldscjiozgdkwefsdljfj_'), alors il y aurait toujours 1 chance sur 26 de trouver le 'c' à cette position, de même pour le 'o', le 'd' et le 'e'. L'espérance de trouver le mot 'code' à cette place est donc la même que celle de le trouver occupant les quatre premières lettres. Il en est de même pour n'importe quelle position. Par exemple, trouver le mot 'code' à la 532ème position avec un saut de 1178 lettres représente aussi 1 chance sur 26 pour chaque lettre, soit 1 chance sur 456 976 en tout.
Nous connaissons l'espérance de trouver le mot 'code' pour n'importe laquelle des positions où il peut apparaître - 1 chance sur 456 976 - et nous disposons du nombre de positions possibles du mot 'code'. Avec ces deux résultats, nous pouvons obtenir la réponse à notre question du départ.
Pour comprendre comment, il suffit de réaliser que chaque position envisageable est une nouvelle possibilité d'obtenir le mot cherché. Comme il y a 15.5 milliards de positions et que 1 fois sur 456 976 (en moyenne) on trouve le mot cherché, comme de plus les positions (bien qu'elles se chevauchent) sont indépendantes, on obtient alors l'espérance de trouver le mot 'code' par le simple calcul suivant :
15 500 000 000 / 456 976 = 33 919
c'est le nombre de fois qu'on peut espérer trouver le mot 'code' écrit dans le sens normal de l'écriture à l'intérieur du texte hasardeux.
Voilà enfin le nombre tant attendu, 33 919 fois ! C'est un grand nombre. Qui aurait cru qu'on pourrait trouver autant de fois ce mot dans un texte de lettres en fouillis, surtout lorsqu'on pense que l'espérance d'obtenir ce mot à un endroit précis semblait infiniment petite.
Comme nous l'avons déjà expliqué, 33 919 ne veut pas dire qu'on trouverait exactement ce résultat, mais qu'on en serait probablement pas très loin (on pourrait même calculer l'espérance qu'il y a de ne pas en être trop éloigné).
Arrivé à ce point, on se rend compte de l'intérêt d'un tel calcul. Nous sommes en mesure de prévoir le nombre d'occurrences de n'importe quel mot dans n'importe quel texte hasardeux. C'est une simple formule qu'on peut calculer avec n'importe laquelle des plus petites calculatrices de poche en quelques secondes. Un peu de réflexion permet de réaliser en peu de temps le travail de plusieurs semaines de recherche intensive sur un ordinateur. On voit nettement l'intérêt des mathématiques lorsqu'on peut prévoir très simplement un résultat difficile.
Le principe du modèle complet
Le fondement
Difficulté mathématique simple
Nous avons vu comment calculer l'espérance d'un mot à l'intérieur d'un texte fait de lettres au hasard. Mais il y a un grand pas entre un texte hasardeux et la Bible (nous employons facilement le mot Bible alors que c'est plus précisément la Torah qui est utilisée dans le livre de Drosnin, c'est-à-dire les 5 premières parties de la Bible). Premièrement, la Bible est écrite en hébreu et non en français, or l'alphabet hébreu ne compte que 22 lettres. La Bible, comme le texte hasardeux que nous avons étudié, est faite d'environ 305 000 lettres, mais ces lettres ne sont pas disposées au hasard. Chaque lettre fait partie d'un mot qui, lui-même, fait partie d'une phrase, puis d'un texte, et ce dernier est inclut dans un des 5 livres de la Torah.
Il se pose un problème important : les mathématiques peuvent uniquement étudier les textes dont les lettres sont hasardeuses, et ce n'est pas le cas du texte biblique ni d'aucun livre sensé d'ailleurs. On pourrait tout simplement considérer le texte biblique comme un des livres de 305 000 lettres parmi les milliards de milliards de livres possibles faits de lettres hasardeuses. Mais peut-on dire que n'importe lequel des livres de 305 000 lettres hasardeuses donnera à peu près les mêmes résultats ? Est-ce que les calculs que nous faisons sont applicables à tous les livres ? Et bien non ! Imaginons un livre qui serait composé de 305 000 lettres 'a'. Il serait impossible d'y trouver le mot 'code'. Or nous avons vu que l'espérance du mot code dans un livre hasardeux est de 33 919 fois. Ce calcul serait clairement inadapté. Mais alors comment peut-on savoir pour quels livres les résultats seront corrects et pour quels livres ils ne le seront pas ? Pour cela, il faut comprendre le sens de nos calculs.
Les calculs que nous faisons ont un sens très précis qui est le suivant : si l'on prenait tous les livres hasardeux possibles, alors la moyenne des résultats de tous les livres serait exactement ce qu'apportent les calculs. Voilà le sens de tous les calculs que nous faisons. Les résultats ne sont valables que pour les livres "moyens", c'est-à-dire pour les livres qui ont des lettres vraiment bien mélangées, sans ordre particulier. En effet, un livre particulier peut très bien être complètement à côté des prévisions : c'est le cas pour un texte qui ne serait composé que de lettres 'a'. Les questions qui suivent sont alors : les livres "moyens" sont-ils les plus nombreux ? La Bible est-elle un livre "moyen" ? Pour répondre à la première question il faudrait donner des explications assez compliquées, mais l'on peut simplement comprendre que les livres particuliers sont pratiquement inexistants par rapport aux livres bien mélangés. Ensuite à la seconde question, "Est-ce que la Bible est un livre moyen ?", la réponse est plus difficile à donner. En effet, il y a une différence fondamentale entre un livre "réfléchi" et un livre hasardeux : dans le livre réfléchi, les lettres sont placées pour former un sens. Est-ce qu'au-delà de ce sens les lettres sont bien mélangées pour pouvoir être considérées comme un livre hasardeux ? La réponse est claire : oui, la Bible pourra être considérée comme un livre bien mélangé, il en est de même pour n'importe quel autre ouvrage. Ainsi, les résultats que nous calculerons correspondront bien à la Bible ou n'importe quel livre. La réponse n'est pas issue d'un calcul, c'est une estimation de mathématiciens objectifs. Cette affirmation correspond précisément à la modélisation du problème. Les modèles mathématiques sont toujours construits sur de telles suppositions. Les modèles sont bons lorsqu'il n'y pas d'autres facteurs importants qui interfèrent pour décaler les résultats des prévisions, ce qui est le cas pour la Bible à une petite précision près que nous allons expliquer.
Il y a en effet une petite remarque à ajouter : toutes les lettres de la Bible n'apparaissent pas avec la même fréquence. Il y a des lettres plus rares et d'autres plus fréquentes ; c'est pourquoi nous ne pouvons pas dire que la Bible est un livre "moyen" dans lequel chaque lettre devrait apparaître de façon similaire. Ainsi nous allons construire un modèle qui prend en compte cette différence d'apparition des lettres en supposant que la distribution des lettres est hasardeuse autour des fréquences définies pour chaque lettre.
En conclusion, l'une des estimations les plus fondamentales du modèle est que nous accepterons que la Bible corresponde bien à livre "moyen" de notre modèle. En effet, tous nos calculs se feront pour un texte dont les lettres sont réparties au hasard. Pour bien comprendre les résultats, il faudra bien comprendre le sens des phrases de la façon suivante : une phrase comme "l'espérance de trouver le mot 'code' dans la Bible est de 34 000 fois" doit être interprétée de la façon suivante : "en recherchant dans tous les différents livres de 305 000 lettres selon le modèle qui est détaillé dans ce livre, la moyenne d'apparition du mot 'code' est de 34 000 fois". C'est là le sens de toutes les estimations que nous donnerons.
Nous verrons si les découvertes sont extraordinaires ou non. En langage mathématique, on dit que les résultats sont significatifs ou non. C'est-à-dire est-ce que les découvertes faites sont tout à fait normales au regard des prévisions ou bien sont-elles prodigieuses ? .
Du texte hasardeux à la Bible
Difficulté mathématique simple
Comme nous venons de le voir, dans le texte de la Bible les lettres ne sont pas choisies complètement au hasard. En particulier, toutes les lettres ne réapparaissent pas avec la même fréquence. En effet, par exemple la lettre å (la lettre hébraïque Waw) apparaît dans près de 10% des cas, soit environ 1 lettre sur 10, alors que la lettre â (la lettre hébraïque Gimel) apparaît à peu près dans 0.7% des cas, c'est-à-dire environ une lettre sur 145 lettres, ce qui est de beaucoup inférieur. On constate ainsi clairement que les lettres ne sont pas équitablement réparties.
Il serait assez grossier de choisir le modèle simpliste que nous avons présenté parce que celui-ci suppose que les lettres apparaissent dans les mêmes proportions. Les mots faits de lettres rares auraient une estimation nettement surévaluée, alors que les mots fait de lettres courantes seraient nettement sous-évalués. Si l'on étudiait une moyenne sur un ensemble vaste de mots, le modèle simpliste serait suffisant. Comme nous allons étudier l'apparition de certains mots précis, il serait très malvenu de choisir ce modèle.
Il faut adapter le modèle au cas précis qu'on étudie : la Bible. Pour cela, il faut tenir compte de la différence d'apparition des lettres. Nous allons transformer notre modèle de la façon suivante : au lieu d'attribuer à toutes les lettres la même espérance d'apparition de 1 sur 22, nous allons établir une espérance spécifique pour chaque lettre. Cette espérance correspondra à son taux d'apparition. Par exemple, la lettre å qui apparaît une fois sur 10 en moyenne se voit attribuer l'espérance de , la lettre â qui apparaît une fois sur 145 se voit attribuer l'espérance de , etc Etant donné que la somme de toutes les lettres constitue le texte, la somme de leur espérance fera 1.
Ce modèle est plus précis, mais il faut bien comprendre ce qu'il signifie : le modèle suppose toujours que nous allons travailler sur des textes hasardeux, mais dont les lettres apparaissent dans une certaine proportion définie. Les résultats que nous obtiendrons devront donc être compris de la façon suivante : si un mot a pour espérance 15, cela signifie qu'en recherchant ce mot dans tous les textes hasardeux (ayant ses fréquences de lettres définis par les fréquences du texte biblique) alors la moyenne serait de 15 apparitions par texte_ On en conclut naturellement que si le texte biblique est bien mélangé, il est fort probable d'y trouver environ 15 fois le mot.
L'espérance d'un mot
Difficulté mathématique assez faible
Il faut adapter les formules que nous avons trouvées sur le nouveau modèle. En fait, la transformation à effectuer n'est pas très compliquée. L'estimation du nombre de positions (donnée par la formule un peu complexe des pages précédentes) reste inchangée. Quelles que soient les lettres du texte, un mot de 4 lettres aura toujours environ 15 500 000 000 milliards de positions possibles dans un texte de 305 000 lettres. La seule nouveauté porte sur l'espérance des lettres.
L'espérance des lettres est plutôt facile à exprimer. Prenons toujours l'exemple du mot 'code' que nous allons hébraïser phonétiquement pour coller au texte biblique. La lettre 'c' ou le 'ë' en hébreu (le kaph) a une espérance de 1 chance sur 25.5 lettres, le 'o' ou le 'å' en hébreu (le waw, la correspondance n'est pas tout à fait naturelle) a une espérance de 1 chance sur 10, le 'd' ou le 'ã' en hébreu (le daleth) a une espérance de 1 chance sur 43.5 lettres, et le 'e' ou le 'ò' en hébreu (le ayin : il n'y a pas exactement de correspondance en hébreu, c'est un choix arbitraire) a une espérance de 1 chance sur 27.1. L'espérance d'obtenir ces quatre lettres 'ëåãò' a une position précise est le produit des quatre espérances énoncées, soit :
1/25,1 x 1/10 x 1/43,5 x 1/27,1= 1/300607. Ceci est l'espérance d'obtenir le mot 'code' (qui n'a pas de sens en hébreu) pour n'importe laquelle des positions possibles.
L'espérance d'obtenir ce mot dans le texte est donnée par le calcul suivant :
15 500 000 000 x 1/300607 = 51562 qui est le produit du nombre de positions possibles par l'espérance d'apparition du mot. Ce nombre est l'espérance d'apparition du mot 'code' (traduit lettre à lettre en hébreu). Ce mot risque d'apparaître autour de 50 000 fois dans le texte biblique.
De cet exemple, on peut tirer une formule générale pour n'importe quel mot dans n'importe quel texte. L'espérance est donnée par le produit du nombre de positions possibles pour un mot multiplié par l'espérance d'apparition de ce mot à un endroit précis. C'est-à-dire pour un mot de longueur m, un texte de longueur T.
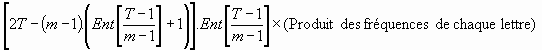
Dans cette formule, on retrouve le premier facteur, le plus élaboré, qui estime le nombre de position ; par contre, le second facteur est nouveau, c'est lui qui prend en compte la spécificité de chaque lettre du mot étudié.
Ce résultat que nous venons de trouver représente l'espérance de trouver un mot donné, par le moyen du saut de lettres, lorsque celui-ci est codé dans le sens de la lecture ; mais comme nous l'avons vu les mots peuvent aussi être codés à l'envers. Il suffit de multiplier par deux le nombre de positions possibles pour en obtenir le nombre total, car chaque position à l'endroit correspond aussi à une position à l'envers. On en déduit la formule suivante :
L'espérance de trouver un mot, à l'endroit ou à l'envers, dans un texte par le procédé du saut de lettre est donc :
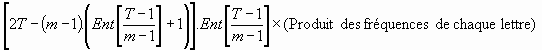 - - m le nombre de lettre du mot cherché
- - m le nombre de lettre du mot cherché
- T la taille du texte
C'est la formule finale que nous utiliserons dans toute notre recherche pour estimer l'apparition d'un mot à l'intérieur du texte Biblique.
Pour pouvoir exploiter cette formule, il suffit juste de connaître l'espérance d'apparition de chaque lettre hébraïque dans la Bible. L'ensemble de ces résultats est consigné dans un tableau que voici :
|
Lettre |
Lettre |
Espérance |
Une lettre sur |
|
ALPEH |
|
0.0887 |
11.3 lettres |
|
BETH |
|
0.0536 |
18.7 lettres |
|
GIMEL |
|
0.0069 |
144.6 lettres |
|
DALETH |
|
0.0231 |
43.4 lettres |
|
HE |
|
0.0920 |
10.9 lettres |
|
WAW |
|
0.1003 |
10 lettres |
|
ZAIN: |
|
0.0072 |
138.8 lettres |
|
RETH: |
|
0.0236 |
42.4 lettres |
|
THET |
|
0.0059 |
169 lettres |
|
YOD: |
|
0.1036 |
9.7 lettres |
|
KAPH |
|
0.0392 |
25.5 lettres |
|
LAMED |
|
0.0707 |
14.1 lettres |
|
MEM |
|
0.0823 |
12.2 lettres |
|
NUN |
|
0.0464 |
21.6 lettres |
|
SAMECH |
|
0.0060 |
166.2 lettres |
|
AYIN |
|
0.0369 |
27.1 lettres |
|
PHE |
|
0.0157 |
63.5 lettres |
|
TSADE |
|
0.0130 |
76.8 lettres |
|
QOPH |
|
0.0154 |
64.9 lettres |
|
RECH |
|
0.0595 |
16.8 lettres |
|
CHIN |
|
0.0511 |
19.6 lettres |
|
TAV |
|
0.0589 |
17 lettres |
III - MESURER LE SECRET
Le Code Secret, comme nous l'avons vu, repose sur un procédé mécanique ; cela présente l'avantage de pouvoir être mesuré par les Mathématiques. Beaucoup d'événements de la vie sont ponctuels et uniques ; dans ce cas il est impossible d'en donner une idée mathématique. Par contre dans le cas du Code Secret, les découvertes sont régies par un mécanisme précis et renouvelable, c'est pourquoi il est possible de mesurer mathématiquement les résultats qu'on obtient.
Il faut tout de même mettre un frein à la confiance absolue dans les chiffres. Les mathématiques, bien qu'elles soient une "science exacte", ne sont exactes que lorsqu'elles parlent d'elles-mêmes, lorsqu'elles restent cantonnées dans la théorie. Mais dès que les mathématiques viennent modéliser la réalité, elles ne sont plus aussi dignes de confiance, car pour établir une simulation il faut construire un modèle qui est toujours un peu différent de la réalité.
Construire un modèle conduit pratiquement toujours à des approximations, des simplifications ; tout simplement parce que la réalité est très complexe dans la plupart des cas. Mais au milieu de la complexité, il y a de nombreux détails qui sont souvent négligeables. Il est souvent inutile de s'y arrêter. Prenons un exemple courant : quand on jette un dé sur un sol plat, on ne se demande pas si le dé peut rester en équilibre sur une arrête ; c'est pourquoi on néglige cette possibilité, mais cela n'est pas une impossibilité certaine. Le modèle mathématique qu'on construit habituellement sur cet exemple dit qu'il y a une chance sur six de tomber sur chaque face, on ne compte pas les autres situations possibles. Heureusement cette approximation est plutôt précise et très proche de la réalité. Pourtant le modèle est simplifié, il est inexact au sens absolu des éventualités possibles. Lorsque un modèle mathématique est posé, le raisonnement et les calculs qui suivent sont toujours exacts si le mathématicien ne fait pas d'erreur. Par contre, il est impossible d'affirmer qu'un modèle colle parfaitement à la réalité. Si le modèle est établit objectivement on pourra tout de même affirmer que l'approximation est très précise. IL ne faudra donc pas s'étonner si l'on procède à quelques simplification qui rende les calculs plus simple sans dénaturer les résultats.
Que faut-il penser de ces remarques ? Il faut simplement toujours être prudent, même avec des mathématiques ; et nous aurons l'occasion de voir pourquoi. Par contre lorsqu'un modèle mathématique est établi et qu'il concorde bien avec la réalité, les résultats sont très fiables. La preuve est qu'on parvient à envoyer des fusées sur la Lune malgré la complexité des phénomènes à prendre en compte.
Il nous reste maintenant à établir le modèle mathématique du Code Secret. Ensuite nous donnerons les résultats issus de ce modèle.
Le modèle mathématique
Chaque titre de chapitre est suivi d'une note sur la difficulté des mathématiques qui y sont contenues. Le lecteur pourra utiliser ces renseignements pour conduire sa lecture.
Le choix du modèle est très important
Difficulté mathématique simple
Nous avons expliqué, et c'est fondamental, que pour calculer un événement, il faut poser un modèle. Voici un exemple : pour aller de Paris à Marseille, il y a 780 km ; en roulant à une moyenne de 120 km/h, il faut 6 heures et demi. Pour établir ce résultat, nous avons fait l'estimation suivante : notre véhicule roulera à 120 km/h. Mais ceci n'est véritablement qu'une estimation théorique. Il est peu probable que notre vitesse puisse constamment être de 120 km/h. Il y a d'un côté le modèle, de l'autre la réalité. On perçoit facilement ce que signifie un tel calcul et chacun saura bien comprendre les écarts entre ce modèle et la réalité. Il en est de même pour les estimations que nous allons établir. Il faut bien comprendre qu'elles apportent un résultat approchant la réalité, mais qui n'est pas significatif de l'exacte réalité qui est inaccessible.
Les choses se compliquent un peu lorsqu'il y a plusieurs façons de poser un modèle mathématique. Lorsqu'un problème n'est pas simple, on peut fréquemment apporter plusieurs explications différentes pour le comprendre. Et bien souvent les différentes approches donnent des résultats dissemblables. En voici un exemple : on lance au hasard, sur une petite table de billard de 1m², une boule de 5cm de diamètre. Supposons qu'on ait tracé une croix au centre de la table, on se pose la question suivante : "Quelle est la probabilité que la boule s'arrête sur la croix ?". Même en supposant que la boule soit vraiment lancée au hasard et qu'elle ait la même chance d'arriver partout sur la table, on peut malgré tout obtenir des résultats complètement différents. Tout dépend de ce qu'on appelle "arriver sur la croix". Si l'on entend par là que l'aplomb du centre de la boule doit être à moins de 0.5mm du centre de la croix - c'est-à-dire très précisément sur la croix - la probabilité est de 1 chance sur 1 273 239. Alors que si l'on accepte que la boule soit à moins de 2.5cm - c'est-à-dire qu'elle soit au-dessus du centre de la croix - alors la probabilité est de 1 chance sur 509. On s'aperçoit de l'énorme différence entre les deux compréhensions du phénomène. Il est fondamental de comprendre cela pour bien interpréter les probabilités. Il faut au départ poser le bon modèle, c'est-à-dire le modèle qui est psychologiquement le plus juste. Quel que soit le choix, il est toujours contestable ; il n'y a pas de modèle absolu. Le rôle du mathématicien est d'être le plus honnête possible pour poser un modèle réaliste. Dans le cas précédent, qu'auriez-vous choisi pour transcrire mathématiquement "arriver sur la croix" ? Est-ce arriver exactement dessus ? C'est mathématiquement impossible en théorie, il est nécessaire d'accepter un seuil de tolérance. Est-ce arriver très près alors ? Dans ce cas, jusqu'à quelle proximité accepte-t-on ? Ce sont des questions importantes, car 1 chance sur 500 et une chance sur 1 million ce n'est pas tout à fait semblable. Il faut donc être très lucide en posant un modèle. Il faut toujours bien comprendre ce que le modèle implique, c'est cela la lucidité indispensable à l'établissement d'un modèle objectif.
L'exemple de la boule, qui est d'un énoncé très simple, pose un problème important de choix du modèle. Heureusement nous n'aurons pas de dilemme aussi compliqué à trancher. Dans l'exemple précédent le problème est compliqué parce qu'on a affaire à des mesures continues (les mesures peuvent prendre toutes les valeurs) ; ce qui n'a pas lieu lorsqu'on ne fait que compter des objets (les résultats ne peuvent être que des valeurs entières). Et mesurer le Code Secret consiste avant tout à compter des objets, comme nous le verrons. Le choix du modèle sera donc moins difficile. Par contre, il restera d'autres questions à trancher.
Avant de commencer le travail fixons bien notre objectif : notre but est de parvenir à estimer les chances de découverte de chacun des tableaux présentés dans "La Bible : le Code Secret".
Probabilité ou Espérance ?
Difficulté mathématique assez simple
La première difficulté est de choisir si l'on va exprimer les résultats en probabilité ou en espérance mathématique. Pour vous ça n'a peut-être aucune importance, étant donné que vous n'en connaissez pas la différence. Comme nous l'avons vu, il est très important de bien comprendre de quoi nous parlons pour pouvoir apprécier les résultats.
Quelle est donc la différence entre une probabilité et une espérance ? Tout d'abord une probabilité est un nombre entre 0 et 1 (à moins que ce ne soit en pourcentage entre 0% et 100%), une probabilité exprime QUAND est-ce qu'une chose arrive. Alors que l'espérance est un nombre positif quelconque, il signifie COMBIEN de fois un événement se produit. Nous allons très vite voir la différence par un cas concret :
Imaginons une Faculté qui possède 10 amphithéâtres. Ils sont tous vides sauf un qui contient 200 personnes.
· Intéressons-nous premièrement à l'espérance : quelle est l'espérance de trouver des gens dans les amphithéâtres ? Cela signifie combien vais-je trouver de personne. Il y a 200 personnes, pour 10 amphithéâtres, l'espérance de trouver des gens est de 20 personnes. C'est la moyenne du nombre de gens que l'on trouve par amphithéâtre.
· Intéressons-nous maintenant à la probabilité : quelle est la probabilité de trouver des gens dans les amphithéâtres ? Cela signifie quand est-ce que je vais trouver quelqu'un ? Et bien, il arrivera que je trouve quelqu'un dans un cas sur 10. La probabilité est de 0.1 (10% de chance).
L'exemple est choisi pour montrer que la différence de résultats entre probabilité et espérance peut être très contrastée. On s'aperçoit en outre que l'utilisation de la probabilité perd des informations : en particulier si le nombre de gens avait été de 3 au lieu de 200, le résultat aurait été le même ; la probabilité ne tient pas compte du nombre, elle tient compte de quand a lieu un événement. L'espérance à l'opposé ne dit pas comment sont répartis les gens dans les amphithéâtres, elle donne seulement une moyenne.
Maintenant que nous avons une petite notion de ce que sont l'espérance et la probabilité, essayons d'aborder un problème un plus proche de notre besoin. L'objet de notre étude est de savoir si un mot choisi peut ou non apparaître dans la Bible par le procédé du saut de lettres. Prenons un exemple simple : observons l'apparition d'une seule lettre. Supposons que nous ayons un livre de 170 pages et que nous voulions y trouver la lettre 'y'. On se pose la question suivante : En ouvrant le livre au hasard, quelle est la chance de trouver la lettre 'y' dans la page ouverte ? La question paraît simple, pourtant il y a plusieurs façons de se poser cette question :
· On peut premièrement se demander quelle est la chance de trouver la lettre 'y' dans la page ouverte ? C'est à dire quel est la chance qu'il y ait au moins un 'y', peu importe le nombre. Cette question correspond à la probabilité ; on désire savoir quand est-ce qu'il y a des 'y'. Pour obtenir ce résultat, il suffit de compter les pages qui n'ont pas de 'y'. Supposons qu'en comptant, nous trouvions 12 pages sans 'y', soit 7 % du livre. La probabilité qui répond à notre question est donc 0.93 ; c'est-à-dire qu'on a 93 chances sur 100 de trouver au moins une fois la lettre 'y'.
· On peut aussi s'intéresser à la question suivante : combien de fois peut-on trouver la lettre 'y' dans une page ouverte au hasard ? En comptant méthodiquement, on s'aperçoit qu'il y a 400 fois la lettre 'y' dans tout le roman. La réponse à notre question est donc simple : on risque de trouver la lettre 'y' 2,35 fois par page en moyenne. L'espérance qui répond à notre question est 2, 35
.
Dans le premier cas, nous avons vu la probabilité de trouver la lettre 'y' ; dans le second, nous avons calculer l'espérance de trouver la lettre 'y'. La différence entre ces deux mesures est claire et précise.
Il nous faut trancher pour savoir quelle mesure utiliser : l'espérance ou la probabilité. Pour choisir, revenons en à notre problème de départ : nous désirons estimer s'il est possible de faire apparaître un mot dans la Bible en sautant des lettres. Or il y a plusieurs façons d'exprimer cette question ; parmi les deux qui suivent laquelle vous paraît la plus intéressante ?
Supposons que nous ayons choisi de rechercher un mot précis à l'intérieur d'un livre.
- Peut-on trouver ce mot dans le livre ?
- Combien de fois peut-on trouver ce mot dans le livre ?
Je crois que la deuxième question est plus intéressante pour nous, car elle nous permet non seulement de connaître si nous pouvons trouver le mot, mais aussi combien de fois nous risquons de le trouver. C'est pourquoi nous exprimerons nos résultats uniquement avec des espérances et non des probabilités qui perdent une partie des résultats.
Il y a une raison supplémentaire à ce choix, c'est que l'espérance se calcule beaucoup plus simplement que les probabilités. Elle sera donc plus facile à comprendre.
Comment faut-il comprendre les résultats ?
En moyenne...
Difficulté mathématique assez simple
Il faudra faire attention en lisant les résultats pour ne pas se méprendre sur ce qu'ils signifient. Lorsqu'on obtiendra une espérance de 3.5, cela signifiera qu'on risque de trouver le mot étudié 3.5 fois. Un résultat de 0.5 signifie qu'on risque de trouver le mot une demi-fois. Mais comment cela est-il possible ? Il faut faire attention : une espérance de 0.5 ne veut pas dire qu'on trouvera le mot cherché une fois sur deux lorsqu'on essaierait de nombreuse fois, mais qu'on trouve le mot une fois sur deux en moyenne. Ce n'est pas la même chose, ce résultat nous dit combien de fois, on peut trouver le mot : une fois sur 2, mais il ne nous dit pas quand on risque de le trouver.
Il ne faut pas confondre les résultats d'une espérance et d'une probabilité, car ils n'ont pas le même sens. Si une probabilité est de 1 (c'est-à-dire 100 %) cela signifie qu'on est sûr de trouver ce qu'on cherche. Mais si une espérance est de 1, il faut faire attention ; cela ne signifie pas qu'on trouvera forcément ce qu'on cherche à tous les coups, mais qu'on le trouve une fois en moyenne, par essai. Si l'espérance est de 1, il se peut que sur 100 essais, on ne trouve ce qu'on cherche que 85 fois (la probabilité serait de 0.85) ; mais dans ce cas il y a forcément dans ces 85 essais, des essais où l'on a trouvé le résultat plusieurs fois, soit deux fois, soit trois fois, etc._ en tout il y a eu 100 résultats positifs.
Lorsque l'espérance est supérieure à 1, il en est de même. Une espérance de 8 signifie qu'on peut espérer voir apparaître ce qu'on cherche 8 fois ; ce résultat est une moyenne sur l'ensemble de tout ce qu'on pourrait essayer.
Faisons une dernière remarque : il arrivera souvent que nous utilisions un abus de langage dont il faut être bien conscient. Lorsqu'on trouve une espérance de 0.2, cela signifie qu'on risque de trouver le résultat recherché 0.2 fois en moyenne sur l'ensemble des recherches, cela signifie qu'en moyenne nous trouverons le résultat une fois sur 5 essais. Cela ne signifie pas que l'on va voir se produire l'événement attendu une fois sur cinq, mais que ses apparitions se font en moyenne une fois sur 5 (pour comprendre cette différence, revenons à un exemple précédent : l'espérance nous disait qu'il y avait 20 personnes par amphithéâtre en moyenne. Ce n'était pourtant pas le cas réel, c'était une moyenne, car les 200 personnes étaient toutes dans le même amphithéâtre) . C'est pourquoi, en parlant d'espérance, lorsqu'on dit : "il y a une chance sur 5 de voir arriver l'événement", il faut bien comprendre que l'on parle de combien et non pas de quand. Une chance sur 5 ne signifie pas une fois sur 5 en constatation , mais une fois sur 5 en moyenne d'apparition. C'est pourquoi en utilisant cette formulation un peu trompeuse, nous ajouterons les mots "en moyenne", afin de bien se rappeler qu'il faut comprendre les résultats en nombre d'apparitions et non pas en moment d'apparition.
De même, lorsque l'espérance de trouver un mot sera de 1 sur 5, il nous arrivera abusivement de dire : "il suffit de faire 5 essais pour espérer trouver le mot", il faudrait ajouter à la fin de cette phrase , "...une fois en moyenne". Car une espérance de 1 sur 5 ne nous dit pas que le résultat arrivera une fois sur cinq essais, mais que la moyenne du nombre des résultats équivaut à ce que le mot apparaisse une fois sur 5, ce qui n'est peut-être pas le cas.
Maintenant, il faut tout de même nuancer un peu cette différence entre probabilité et espérance: par exemple lorsqu'un calcul, nous donnera une faible espérance comme 1 sur 100, il arrivera en général que le mot ayant cet espérance apparaissent aussi une fois sur 100 en pourcentage d'essais (cela signifie qu'un mot ayant une espérance de 1 sur 100 possède aussi une probabilité de 1 sur 100, ou très légèrement moins). En effet, on pourrait montrer que dans les exemples que nous rechercherons, lorsque l'espérance est faible, elle possède une valeur très proche de la probabilité. Cela vient du fait que les événements que nous allons étudier sont, en général, uniformément répartis, c'est à dire que les résultats ne sont pas concentré sur certains essais (pour reprendre l'exemple du départ, on ne trouverait jamais 200 élèves dans un amphithéâtre, et aucun ailleurs). Cette constatation permet donc d'atténuer la gravité du contresens qui est fait lorsqu'on interprète une espérance de 0.1 en disant que l'événement arrive une fois sur 10. Pour résumer cette dernière idée, disons que la confusion entre espérance et probabilité n'est pas très dommageable quand les résultats sont faibles.
Au pire...
Il convient aussi de bien expliquer un autre principe important dans le calcul des espérances. Imaginons l'expérience suivante : on bande les yeux d'un homme qu'on fait entrer dans une pièce ronde ; on lui annonce que sur le mur de 9 mètres de circonférence se trouve tracé un trait vertical que l'homme ne voit pas. L'expérience consiste à donner une épingle à cet homme afin qu'il la plante dans le mur, en espérant qu'il se rapproche au maximum du trait. Supposons maintenant qu'un essai donne le résultat suivant : un candidat a planté l'épingle à 3,75 cm du trait. C'est un résultat remarquable : en supposant que l'homme puisse planter l'épingle n'importe où dans le mur de façon indifférente, un pareil résultat ne se produit qu'une fois sur 120 ( en effet 900cm / ( 3.75cm x 2 ) = 120, le coefficient 2 vient du fait qu'il peut être d'un coté ou de l'autre du trait). Un résultat ayant une valeur de 1 chance sur 120 est assez remarquable.
Soyons plus précis : l'épingle a été planté à 3.75 cm du trait, le fait de planter au hasard une épingle à la distance exacte de 3.75cm est un événement pratiquement impossible. Car si l'on mesure la distance avec une grande précision, il y a très peu de chance de planter l'épingle exactement à cet endroit : à 3.75 cm du trait ; il en est de même d'ailleurs pour toutes les autres positions. N'importe laquelle des positions où l'on peut planter l'épingle est pratiquement impossible. Cela provient du fait que les positions éventuelles sont innombrables (presque infinies en théorie). Ainsi chacune d'elle est presque impossible. La question subséquente est donc : comment mesurer la probabilité que l'aiguille arrive à 3.75 cm, si cette probabilité est pour ainsi dire nulle ?
Si l'on revient maintenant à l'expérience, ce qui nous intéresse ce n'est pas que l'épingle soit exactement à 3.75 cm du trait, mais qu'elle soit le plus proche possible du trait. Pour mesurer le fait que l'aiguille soit plantée à 3.75 cm du trait, on ne mesurera pas la probabilité de tomber exactement à 3.75 cm, mais la probabilité de tomber au maximum à 3.75 cm, c'est-à-dire la probabilité que l'aiguille tombe AU PIRE à 3.75cm. La mesure ainsi obtenue correspond bien à l'impression psychologique : "planter l'aiguille assez près du trait" (à une proximité de 3.75 cm).
C'est un principe constant dans toutes les mesures de probabilités ayant rapport aux phénomènes continus. On ne mesure la probabilité qu'un événement arrive exactement comme on l'a vu se produire, mais la probabilité qu'il arrive au pire comme on l'a vu se produire. Si l'on s'arrête un peu sur ce principe, on s'aperçoit que c'est la meilleure, sinon la seule façon de procéder. Il faut être conscient de ce principe pour bien interpréter des résultats.
C'est ce principe de mesure que nous allons utiliser pour énoncer les résultats que nous chercherons. En particulier lorsque nous chercherons à mesurer l'apparition de plusieurs mots se croisant dans un même tableau. Nous ne donnerons pas l'espérance de trouver exactement les mots considérés à la place qu'ils occupent, mais plutôt l'espérance de trouver un résultat qui ait au pire une impression psychologique similaire. Ceci donnera la mesure du tableau.
Si pour un tableau particulier nous trouvons une espérance de 15, cela signifiera qu'on peut trouver en moyenne au moins 15 tableaux similaires OU MIEUX ENCORE. Voilà le sens précis qu'il faudra donner aux résultats que nous trouverons.
Plan de recherche
Avant de rentrer dans le vif du sujet, prenons le temps de fixer quelle sera notre démarche, afin de toujours garder un fil conducteur pour toutes les explications et démonstrations que nous allons effectuer. Ce plan permettra au milieu d'un dédale d'explications de se souvenir du but à atteindre.
Essayons de comprendre quel est le but de notre recherche : nous désirons pouvoir mesurer si les tableaux du livre de Drosnin sont le résultat naturel du hasard, ou si leur présence est mathématiquement inexplicable. Nous avons vu que pour établir ces résultats il faut mesurer chaque tableau au moyen des Espérances Mathématiques. Les résultats obtenus nous permettrons de savoir si les tableaux sont issus d'un mécanisme naturel ou non, suivant que les espérances trouvées sont assez élevées, ou bien très faibles. Il nous reste donc à savoir comment calculer l'espérance d'un tableau. C'est le but de toute notre recherche.
Le modèle mathématique qui permet d'évaluer les tableaux doit être calqué sur le mécanisme utilisé pour construire ces tableaux. Or nous avons vu que la méthode la plus simple pour faire apparaître des mots qui se croisent est de rechercher premièrement le mot principal. Lorsque celui-ci - (ou ceux-ci lorsqu'on trouve plusieurs mots principaux possibles) - est découvert, il faut alors rechercher si l'on peut trouver le premier mot satellite à la périphérie du mot principal. Lorsque le premier mot satellite est découvert, on peut ensuite chercher si l'on trouve d'autres mots satellites, à proximité des deux premiers.
1. C'est ainsi que nous cherchons d'abord à déterminer l'espérance d'un mot principal (ou d'un mot seul, ce qui revient au même). C'est la première partie de notre recherche traiter dans le paragraphe : "Mesurer la découverte d'un mot".
2. Ensuite nous chercherons à déterminer l'espérance de découvrir un premier mot satellite à proximité d'un mot principal qui a déjà été trouvé. Cela sera traité dans la partie : "Mesurer la découverte du deuxième mot".
3. Lorsqu'on a mis en évidence deux mots qui se croisent, on peut chercher à faire apparaître un troisième mot, un quatrième mot, etc_ Nous aborderons cela dans la partie intitulée : "Mesurer la découverte des mots suivants".
Le premier point est le plus facile à traiter, le second est probablement le plus difficile et la troisième partie suit assez logiquement la deuxième partie.
Le modèle que nous allons construire est loin d'être le seul qui puisse mesurer les tableaux. Par contre selon le procédé de recherche que nous avons établi, qui consiste à chercher les mots les uns après les autres, le modèle sera parfaitement adapté et permettra de mesurer réellement les tableaux construits selon cette chronologie.
Nous avons bien précisé que le modèle doit se calquer sur la méthode avec laquelle on recherche les tableaux, mais si les tableaux ont été découverts par une autre méthode, est-ce que le modèle convient encore ? En particulier, les exemples de tableaux que nous avons conçus dans les chapitres précédents n'ont pas été construits selon la méthode que nous expliquons qui consiste à rechercher le mot principal, puis les mots satellite, etc... Tous les tableaux que nous avons découverts dans le livre de Pascal, ou dans le livre fait de lettres tirées au hasard sont le fruit d'un programme informatique qui utilise une méthode plus performante. La méthode consiste à analyser toutes les positions de chacun des mots recherchés et produire les meilleurs tableaux où ceux-ci se croisent.
Notre modèle est-il alors inadapté pour mesurer des tableaux qui n'ont pas été construits selon la logique chronologique du modèle que nous exposons ? La réponse est évidemment négative, notre modèle pourra mesurer tous les tableaux ; seulement, les espérances obtenues se rapporteront à la méthode de recherche chronologique (recherche du mot principal d'abord, puis premier mot satellite ensuite, etc...). En effet, il est possible de rechercher n'importe quel tableau par cette méthode chronologique, il est donc aussi possible de mesurer tous les tableaux avec le modèle que nous allons construire. Il faut remarquer par ailleurs qu'il est possible que les espérances que nous trouvions par notre modèle soient sous-évaluées. Cela provient du fait qu'en disposant d'une méthode de recherche plus efficace, on augmente les chances de découverte.
Si les résultats sous-évalués sont une preuve - et nous verrons qu'ils le sont - à combien plus forte raison des résultats plus précis le seraient aussi. En fait, on peut s'apercevoir qu'en choisissant une méthode ou bien une autre, la différence des résultats n'est pas flagrante. Il convient donc d'essayer de construire un modèle qui privilégie la simplicité. Malheureusement la simplicité reste toujours bien relative_
Mesurer la découverte d'un mot
Nous voilà fixés sur la façon de présenter les résultats et sur la façon dont il faut les comprendre. Il nous reste à faire le plus difficile maintenant, c'est fixer le modèle.
Modèle de base
Difficulté mathématique simple
Nous allons d'abord construire un modèle simplifié afin de comprendre comment fonctionne les calculs ; ensuite nous poserons un modèle plus réaliste qui donne des résultats plus précis.
Posons clairement le problème : notre but est de déterminer l'espérance d'apparition d'un mot quelconque dans la Bible. Il serait par exemple intéressant de trouver si notre nom se trouve dans la Bible. Choisissons un mot pour fixer les idées, le mot 'code'. Ce mot existe-t-il ? Est-il caché par le Code Secret dans le texte biblique ? Il faut le décoder. Il faut trouver si, en sautant des lettres, il est possible de le faire apparaître. Ce mot existe-t-il ? Et s'il existe, combien de fois peut-on le trouver dans la Bible ? Il est entièrement possible de prévoir cela mathématiquement, c'est ce que nous allons découvrir. On pourrait utiliser un ordinateur pour voir si le mot s'y trouve ; un ordinateur assez puissant de préférence, car cette recherche risque d'être assez longue. Seulement cela ne nous dit toujours pas si ce que nous trouvons est normal ou non. C'est pourquoi il est encore plus intéressant de prévoir le résultat mathématiquement.
Avant de travailler sur la Bible, nous allons travailler sur un autre texte afin de comprendre comment fonctionne cette recherche. Nous allons utiliser un texte avec des lettres françaises, c'est plus facile à comprendre. Supposons de plus que le texte ne signifie absolument rien. C'est un ordinateur qui aurait tiré des lettres au hasard sans aucun sens, sans même aucun espace entre les lettres. Quelque chose de ce genre :
"onoeemsleneemntrrdosuutclgeiuuraainenennmuueenumrdosstomepereanreeoeuesuelrnblhseunoiouaieeilveileqeovtetmaiiodeeouiieoaueosmdpclooeuuuadecucevaclrtnfaeseeimsdsasssdeurenepecooeluttsuuisblataeeutaietetvoeaaeccvfandutaeirledeeutthhobdlopesslreaaetlmnonudsucandnrnnanhescevartpsesrrisssseuinetuoimiemaicpaerlletticlimqaitmeeeemotrmseuetdleruvlnkmaeaessllninsetdostenpoiluedeeumipaesultsiaiitatilseulltleeadeiettesaeieeoselidneseurimsvslebsanegeeqeletuumefdneaoscaasettuuessedsastvmreantoaerdliosctsaitetemnrolutpeoolanrrurqscuoansrelmieltuhenjdiusuuscpsdnrereaelnossmrerumelcuceeeuuceuepcsjuvoozoiluetoatutnoemeioag"
Mais au lieu de quelques lignes, nous supposerons que nous disposons de tout un livre de 305 000 lettres, car c'est à peu près ce nombre de lettres que contient le texte de la Bible utilisée pour les recherches du Code Secret. Ce serait un livre pas vraiment intéressant en soi_ Par contre, il va nous être bien utile pour comprendre ce que nous désirons connaître.
Pour une seule lettre
Difficulté mathématique simple
Nous allons simplement commencer par chercher si nous pouvons trouver dans notre fameux livre la première lettre du mot 'code', la lettre 'c'. Quelle est l'espérance de trouver cette lettre 'c' dans le texte ? Ce calcul est très simple. Etant donné qu'il y a vingt six lettres dans l'alphabet français et qu'on a supposé le texte composé de lettres au hasard, alors la lettre 'c' sort une fois sur 26 en moyenne. Comme il y a 305 000 lettres, cela fait une espérance de lettres. Cela ne veut pas dire qu'il y a forcément 11 731 lettres 'c' dans le texte. D'ailleurs en comptant le nombre de 'c' dans des milliers de livres différents fabriqués avec 305 000 lettres au hasard, il y aurait extrêmement peu de livre où l'on trouverait exactement 11 731 fois la lettre 'c'. Par contre, on s'apercevrait que la plupart des fois le nombre de lettre 'c' est assez proche de 11 731. On s'apercevrait même d'une chose plutôt surprenante : En faisant la moyenne des résultats trouvés, on obtiendrait exactement 11 731 (si on a compté sur un assez grand nombre de livre). C'est un résultat que les mathématiques peuvent prévoir.
Ceci est un résultat très important qui est à la base de tous les calculs que nous allons faire. On pourrait exprimer ce résultat à peu près ainsi : lorsqu'on répète un très grand nombre de fois une expérience, la moyenne des résultats s'approche de plus en plus de l'estimation calculée (si la modélisation a été bien faite). Pour preuve, nous vous proposons de faire l'expérience suivante : lançons un dé un très grand nombre de fois, et intéressons-nous aux valeurs obtenues par le dé : les valeurs qui peuvent apparaître sont le 1, le 2, etc_ jusqu'à 6. L'expérience consiste calculer la moyenne de tous les résultats obtenus. Par exemple si en jetant le dé 14 fois nous obtenons les résultat suivants : 3, 4, 6, 1, 2, 2, 5, 3, 4, 5, 1, 3, 2, 4, nous dirons que la valeur moyenne des résultats est de (3+4+6+1+2+2+5+3+4+5+1+3+2+4)/6=3.21. Quel est l'intérêt de cette expérience ? C'est de montrer que le mathématique permettent de prévoir exactement la moyenne lorsque le nombre de lancers de dé est suffisamment grand. En effet, que si nous réitérons un grand nombre de lancer de dé, nous pouvons affirmer que nous trouverons une moyenne proche de 3.5. En voici la raison : chaque numéro de 1 à 6 sur le dé à la même chance d'apparaître qui est de 1 chance sur 6. Ainsi, sur un très grand nombre de lancers, chacun des chiffres de 1 à 6 apparaîtra un nombre de fois à peu près identique par exemple chacun environs 150 fois. On peut obtenir par exemple 145 fois le 1, 154 fois le 2, 138 fois le 3, 161 fois le 4, 152 fois le 5 et 149 fois le 6. La moyenne des points obtenus sera donc (145x1+154x2+138x3+161x4+152x5+149x6)/(145+154+138+161+152+149)=3.52. Lorsqu'on joue un très grand nombre de fois le dé, les différentes faces apparaissent un nombre de fois à peu près égales. Si on considérait qu'en jouant un très grand nombre de fois le dé, les faces apparaissaient un nombre de fois exactement égales, on pourrait simplifier le calcul de la moyenne en calculant directement la moyenne des valeurs du dé ; c'est-à-dire par le calcul suivant : (1+2+3+4+5+6)/6=3.5 . C'est exactement le résultat vers le quel tend la moyenne lorsqu'on joue indéfiniment. Il faudra être patient, car pour être sûr d'obtenir ce résultat, il faudrait lancer le dé un nombre de fois très important. Et plus on veut un résultat proche de 3.5, plus il faudra lancer le dé un grand nombre de fois. En théorie, en jouant sans s'arrêter, on pourrait aller aussi près qu'on veut de 3.5 si l'on est assez patient (et si les dés sont parfaitement équilibrés).
L'intérêt de cette expérience permet de montrer que lorsqu'on peut produire une expérience un grand nombre de fois, les mathématiques peuvent très souvent prévoir le résultat moyen de ces expérience. C'est exactement le type de problème auquel on a affaire avec le Code secret.
Pour plusieurs lettres
Difficulté mathématique assez simple
Nous avons étudié la lettre 'c'. Maintenant nous allons renouveler la même étude pour tout le mot 'code'. Combien de fois peut-on espérer le trouver dans notre fameux livre ? Souvenons-nous que ce livre est fabriqué de lettres au hasard. Il se pourrait par exemple qu'on trouve le mot 'code' au tout début, dans les quatre premières lettres du livre. Comme les lettres sont tirées au hasard et qu'il y en 26, l'espérance de trouver la lettre 'c' en première position est de 1/26. Mais l'espérance de trouver la lettre 'o' exactement en deuxième position est aussi de 1/26, car les 26 lettres ont la même espérance d'être à cette deuxième position, comme à n'importe quelles positions d'ailleurs. A chaque position on peut trouver n'importe quelle lettre.
La question qui suit est de savoir quelle est l'espérance de trouver la lettre 'c' en première position en même temps que la lettre 'o' en deuxième position. Pour comprendre cela, il faut voir qu'il y a 1 chance sur 26 d'avoir le 'c' en première position ; c'est-à-dire que sur 26 livres différents, il y en a un seul en moyenne où le 'c' est en première position ; Ou encore, sur 676 (= 26 x 26) livres il y en a 26. Puis il faut le 'o' en seconde position, c'est-à-dire à nouveau une chance sur 26. Sur les 676 cas au départ, il n'y en a que 26 où la lettre 'c' est en première position. Sur ces 26 livres, il n'y en a qu'un qui ait le 'o' en deuxième position. Il y a donc un seul livre en moyenne sur les 676 où les deux premières lettres sont 'co'. On constate que l'espérance d'avoir les deux lettres au début est tout simplement le produit des espérances de chaque lettre. On obtient le résultat par le calcul suivant (1/26 x 1/26 = 1/676).
Ce résultat se généralise en une loi mathématique : si l'on veut obtenir en même temps deux résultats indépendants (c'est-à-dire qui ne se gênent pas l'un et l'autre en quelque sorte), il suffit de multiplier les espérances de chacun d'eux pour obtenir l'espérance des deux réunis.
Par ce principe, on obtient facilement l'espérance d'obtenir le mot 'code' dans les quatre premières lettres du livre : (1/26 x 1/26 x 1/26 x 1/26 = 1/456976), c'est un résultat très faible, 1 chance sur 456976. Il faut comprendre que sur 456 976 livres fabriqués avec des lettres au hasard, nous risquons d'en trouver 1 seul dont les quatre premières lettres sont 'code'. Autant dire qu'il faudrait de la patience_ Ce nombre est si faible que nous pourrions nous demander s'il est même possible de trouver le mot 'code' dans la Bible, même le moyen du saut de lettres qui ne fait qu'augmenter un peu les chances,_ nous verrons.
Les positions possibles
Difficulté mathématique un peu plus élevée
Notre problème n'est pas encore résolu. Notre question était : combien de fois peut-on espérer trouver le mot 'code', non pas au début mais n'importe où dans le texte, même en sautant des lettres. Là encore les choses se corsent un petit peu plus. Nous allons décomposer le problème.
Pour une taille de saut déterminée
La première question qui va nous intéresser est de savoir à combien de positions différentes le mot 'code' peut apparaître. La réponse est : un bon paquet ! Pour les compter, il faut les rechercher méthodiquement.
Le mot peut apparaître en première position, comme nous l'avons vu. Il peut aussi apparaître en deuxième position, c'est-à-dire en commençant à la 2ème lettre du texte. Par exemple si le livre commençait par 'wcodekjhfhsdfjd_', on dirait que le mot 'code' apparaît en 2ème position. Ensuite, il peut apparaître à la 3ème, la 4ème, la 5ème position_ jusqu'à la 304 997ème position. En effet, la dernière position possible pour la lettre 'c' n'est pas dernière lettre du texte, car il y a encore trois lettres derrière. Regardons la fin d'un texte dans un exemple : '_qsdfjkljcode'. En sachant que le texte a 305 000 lettres, on s'aperçoit que le 'c' est à la 304 997ème position. On obtient un total de 304 997 positions possibles pour le mot 'code' écrit en lettres collées.
Maintenant si on prend une lettre toutes les deux lettres et qu'on voit apparaître le mot 'code' - c'est le cas par exemple dans le texte suivant : '_fdkhfpoickoedlemkffdij_'. - on dira que le mot 'code' apparaît avec un saut de 2 lettres. On peut se demander combien de fois le mot 'code' peut apparaître de cette façon dans 305 000 lettres. Pour un saut de 2 lettres, la lettre 'c' peut à nouveau être à la 1ère position, à la 2ème,à la 3ème, etc._ jusqu'à la 305 000 - 6 = 304 994ème position, car 6 est la place nécessaire pour que le mot code puisse apparaître avec un saut de 2 lettres. Ceci fait à nouveau 304 994 positions possibles pour le mot 'code'.
Il y encore les cas où le mot apparaîtra avec un saut de 3 lettres, de 4 lettres, etc. Imaginons un saut de 600 lettres : combien de positions sont possibles ? La 1ère position est possible, la 2nde aussi, la 3ème également, etc_ jusqu'où ? Il faut commencer à compter précisément : le mot 'code' est fait de 4 lettres ; s'il apparaît dans le livre avec un saut de 600 lettres, cela veut dire qu'entre le 'c' et le 'o' il y a 599 autres lettres, de même entre le 'o' et le 'd' puis entre le 'd' et le 'e'. Le mot occupe une place totale de 1+599+1+599+1+599+1=1801 lettres. On peut donc trouver la dernière position possible pour le mot 'code' en saut de lettres 600. Cette dernière position est 305 000 - 1800 = 303 200. En effet il faut retirer 1800 à 305 000, et non pas 1801, car il ne faut pas retirer le 'c' puisque c'est lui qu'on essaie de placer.
Passons maintenant à une explication un petit peu plus compliquée. Au lieu de refaire les mêmes calculs pour chaque taille de saut différent, on va essayer de construire une formule. Pour cela on va utiliser des lettres à la place des chiffres. On va dire que le mot 'code' apparaît avec un saut de s lettres, (s comme saut). Le nombre de saut s, peut prend une valeur quelconque : 3, 5, 180 ou 15 384_ Cela n'a aucune importance. Ce chiffre, quel qu'il soit, sera noté par s.
Notre première question est : pour un saut de s lettres, quelle place occupe le mot 'code' dans le texte ? Entre le 'c' et le 'o', il y a s-1 autres lettres, de même entre le 'o' et le 'd' puis entre le 'd' et le 'e'. Le mot occupe une place totale de 1 + ( s-1 ) + 1 + ( s-1 ) + 1 + ( s-1 ) + 1 = 3 s + 1.
La seconde question est : combien de positions sont possibles pour le mot 'code' avec un saut de s lettres ? Selon le même raisonnement que précédemment 305 000 - 3s (car il ne faut pas ôter la première lettre 'c'). D'où vient le nombre 3 dans cette formule ? Le mot 'code' est fait de quatre lettres. Pour un mot de quatre lettres, il y a 3 intervalles entre les lettres : entre le 'c' et le 'o', entre le 'o' et le 'd', puis entre le 'd' et le 'e'. Le chiffre 3 est tout simplement le nombre de lettres moins une : 4 -1.
Pour un mot de 10 lettres, on pourrait refaire le même calcul. Pour qu'il apparaisse parmi les 305 000 lettres du texte avec un saut de s lettres, il y a 305 000 - 9s positions possibles.
On obtient finalement la formule suivante :
- pour un mot de m lettres,
- avec des sauts de s lettres,
- dans un texte de T lettres,
On obtient :
T - (m-1).s positions possibles.
Quelle taille de saut maximale ?
Nous savons calculer combien il existe de positions possibles pour chaque saut. Mais il reste une question importante : jusqu'à quelle taille de sauts peut-on aller ? Quelle est la taille du saut maximal ? Prenons comme exemple le mot 'mystérieux', il comprend 10 lettres. On peut chercher en tâtonnant : avec un saut de 33 889 lettres, le mot occupe une place de 33 889 x 9 + 1 = 305 002 lettres : c'est trop. Le plus grand saut possible est donc de 33 888 lettres. Mais comment trouver ce nombre de façon mécanique ? On a vu que, pour un saut de s lettres, le mot occupait une place de 9 x s + 1 lettres ; il suffit simplement que 9 x s + 1 £ 305 000, c'est-à-dire que 9 x s £ 305 000 -1 puis en divisant par 9 que s£(30500-1)/9, or (30500-1)/9= 33 888,7777... Donc s, qui est forcément un nombre entier, vaut au maximum 33 888 .
On peut généraliser ce calcul par le même raisonnement :
- pour un texte de T lettres,
- pour un mot de m lettres,
- pour un saut de s lettres,
La saut maximale est le plus grand nombre entier inférieur ou égal à (T-1)/(m-1), qui sera noté: Ent[(T-1)/(m-1)] avec Ent pour dire entier.
Nous avons construit les deux formules essentielles qui vont nous permettre de déterminer ce que nous cherchons. Qu'est-ce qu'on cherchait d'ailleurs ? Ah oui ! Le nombre total de positions possibles totales pour le mot 'code' dans un texte farfelu de 305 000 lettres.
Nombre total de positions
Nous savons déterminer pour chaque saut de s lettres combien il y a de positions possibles. Nous savons de plus que les sauts peuvent varier de 1 (pour des lettres collées) jusqu'à Ent[(T-1)/(m-1)]. Et bien il ne reste plus qu'à calculer la somme de ces positions possibles.
Si on a un texte de taille T, un mot de taille m, le nombre de positions possibles est donc :
[ T - (m-1).1 ] + [ T - (m-1).2 ] + [ T - (m-1).3 ] + . . .+ [ T - (m-1). ]
Il est possible de simplifier cette expression en utilisant une astuce mathématique. On pose l'opération en prenant deux fois cette somme, une fois à l'endroit et une fois à l'envers :
shapeType20fFlipH0fFlipV0lineColor13948116lineWidth0shadowOffsetX0shadowOffsetY-12700shadowOriginY32385fShadow1
[ T - (m-1).1 ] + [ T - (m-1).2 ] + . . .+ [ T - (m-1). ( Ent[(T-1)/(m-1)]-1) ] + [ T - (m-1).Ent[(T-1)/(m-1)] ] +
[ T - (m-1).Ent[(T-1)/(m-1)] ] + [ T - (m-1). (Ent[(T-1)/(m-1)] -1)] + . . .+ [ T - (m-1).2 ] + [ T - (m-1).1 ]
= [2.T - (m-1). (Ent[(T-1)/(m-1)] +1)] + [ 2.T - (m-1). (Ent[(T-1)/(m-1)] +1)] + . . .+ [2.T - (m-1). (Ent[(T-1)/(m-1)]+1)] + [ 2.T - (m-1).Ent[(T-1)/(m-1)] +1)]
Par cette astuce, en regroupant les sommes par deux, on trouve à chaque fois la même somme. On la trouve en tout Ent[(T-1)/(m-1)] fois. Ainsi la double somme est égale à :
= [ 2T - (m-1). (Ent[(T-1)/(m-1)]+1)] .Ent[(T-1)/(m-1)] , ce résultat vaut deux fois la somme totale qu'on cherche. Il suffit de diviser par 2. La somme qui nous intéresse est donc donnée par la formule suivante :
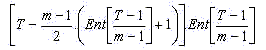
Ceci est le nombre de positions possibles pour un mot de longueur m dans un texte de longueur T constitué de lettres alignées au hasard et avec tous les sauts de lettre possibles permis.
Notre question était : à combien de positions différentes peut-on trouver le mot 'code' dans un texte de 305 000 lettres ? La réponse est donc:
![]()
Voici le résultat tant attendu. Nous naviguons dans les grands nombres. Pour avoir une idée plus précise de ce que signifie ce nombre : avec 15 500 000 000 oranges placées côte à côte, nous ferions plus de 27 fois le tour de la terre_ c'est donc un très grand nombre.
La réponse pour plusieurs lettres
Difficulté mathématique assez simple
Il est maintenant temps de répondre à la question initiale, celle qui nous intéressait en premier lieu : combien de fois peut-on espérer trouver le mot 'code' dans un texte hasardeux de 305 000 lettres ?
Nous avons vu que l'espérance de trouver le mot 'code' dans les 4 premières lettres était de 1 chance sur 456 976. Or si, au lieu de le trouver occupant les quatre premières lettres, on désirait le trouver en 4ème position avec un saut de 3 lettres (comme ici dans le texte suivant : 'ldscjiozgdkwefsdljfj_'), alors il y aurait toujours 1 chance sur 26 de trouver le 'c' à cette position, de même pour le 'o', le 'd' et le 'e'. L'espérance de trouver le mot 'code' à cette place est donc la même que celle de le trouver occupant les quatre premières lettres. Il en est de même pour n'importe quelle position. Par exemple, trouver le mot 'code' à la 532ème position avec un saut de 1178 lettres représente aussi 1 chance sur 26 pour chaque lettre, soit 1 chance sur 456 976 en tout.
Nous connaissons l'espérance de trouver le mot 'code' pour n'importe laquelle des positions où il peut apparaître - 1 chance sur 456 976 - et nous disposons du nombre de positions possibles du mot 'code'. Avec ces deux résultats, nous pouvons obtenir la réponse à notre question du départ.
Pour comprendre comment, il suffit de réaliser que chaque position envisageable est une nouvelle possibilité d'obtenir le mot cherché. Comme il y a 15.5 milliards de positions et que 1 fois sur 456 976 (en moyenne) on trouve le mot cherché, comme de plus les positions (bien qu'elles se chevauchent) sont indépendantes, on obtient alors l'espérance de trouver le mot 'code' par le simple calcul suivant :
15 500 000 000 / 456 976 = 33 919
c'est le nombre de fois qu'on peut espérer trouver le mot 'code' écrit dans le sens normal de l'écriture à l'intérieur du texte hasardeux.
Voilà enfin le nombre tant attendu, 33 919 fois ! C'est un grand nombre. Qui aurait cru qu'on pourrait trouver autant de fois ce mot dans un texte de lettres en fouillis, surtout lorsqu'on pense que l'espérance d'obtenir ce mot à un endroit précis semblait infiniment petite.
Comme nous l'avons déjà expliqué, 33 919 ne veut pas dire qu'on trouverait exactement ce résultat, mais qu'on en serait probablement pas très loin (on pourrait même calculer l'espérance qu'il y a de ne pas en être trop éloigné).
Arrivé à ce point, on se rend compte de l'intérêt d'un tel calcul. Nous sommes en mesure de prévoir le nombre d'occurrences de n'importe quel mot dans n'importe quel texte hasardeux. C'est une simple formule qu'on peut calculer avec n'importe laquelle des plus petites calculatrices de poche en quelques secondes. Un peu de réflexion permet de réaliser en peu de temps le travail de plusieurs semaines de recherche intensive sur un ordinateur. On voit nettement l'intérêt des mathématiques lorsqu'on peut prévoir très simplement un résultat difficile.
Le principe du modèle complet
Le fondement
Difficulté mathématique simple
Nous avons vu comment calculer l'espérance d'un mot à l'intérieur d'un texte fait de lettres au hasard. Mais il y a un grand pas entre un texte hasardeux et la Bible (nous employons facilement le mot Bible alors que c'est plus précisément la Torah qui est utilisée dans le livre de Drosnin, c'est-à-dire les 5 premières parties de la Bible). Premièrement, la Bible est écrite en hébreu et non en français, or l'alphabet hébreu ne compte que 22 lettres. La Bible, comme le texte hasardeux que nous avons étudié, est faite d'environ 305 000 lettres, mais ces lettres ne sont pas disposées au hasard. Chaque lettre fait partie d'un mot qui, lui-même, fait partie d'une phrase, puis d'un texte, et ce dernier est inclut dans un des 5 livres de la Torah.
Il se pose un problème important : les mathématiques peuvent uniquement étudier les textes dont les lettres sont hasardeuses, et ce n'est pas le cas du texte biblique ni d'aucun livre sensé d'ailleurs. On pourrait tout simplement considérer le texte biblique comme un des livres de 305 000 lettres parmi les milliards de milliards de livres possibles faits de lettres hasardeuses. Mais peut-on dire que n'importe lequel des livres de 305 000 lettres hasardeuses donnera à peu près les mêmes résultats ? Est-ce que les calculs que nous faisons sont applicables à tous les livres ? Et bien non ! Imaginons un livre qui serait composé de 305 000 lettres 'a'. Il serait impossible d'y trouver le mot 'code'. Or nous avons vu que l'espérance du mot code dans un livre hasardeux est de 33 919 fois. Ce calcul serait clairement inadapté. Mais alors comment peut-on savoir pour quels livres les résultats seront corrects et pour quels livres ils ne le seront pas ? Pour cela, il faut comprendre le sens de nos calculs.
Les calculs que nous faisons ont un sens très précis qui est le suivant : si l'on prenait tous les livres hasardeux possibles, alors la moyenne des résultats de tous les livres serait exactement ce qu'apportent les calculs. Voilà le sens de tous les calculs que nous faisons. Les résultats ne sont valables que pour les livres "moyens", c'est-à-dire pour les livres qui ont des lettres vraiment bien mélangées, sans ordre particulier. En effet, un livre particulier peut très bien être complètement à côté des prévisions : c'est le cas pour un texte qui ne serait composé que de lettres 'a'. Les questions qui suivent sont alors : les livres "moyens" sont-ils les plus nombreux ? La Bible est-elle un livre "moyen" ? Pour répondre à la première question il faudrait donner des explications assez compliquées, mais l'on peut simplement comprendre que les livres particuliers sont pratiquement inexistants par rapport aux livres bien mélangés. Ensuite à la seconde question, "Est-ce que la Bible est un livre moyen ?", la réponse est plus difficile à donner. En effet, il y a une différence fondamentale entre un livre "réfléchi" et un livre hasardeux : dans le livre réfléchi, les lettres sont placées pour former un sens. Est-ce qu'au-delà de ce sens les lettres sont bien mélangées pour pouvoir être considérées comme un livre hasardeux ? La réponse est claire : oui, la Bible pourra être considérée comme un livre bien mélangé, il en est de même pour n'importe quel autre ouvrage. Ainsi, les résultats que nous calculerons correspondront bien à la Bible ou n'importe quel livre. La réponse n'est pas issue d'un calcul, c'est une estimation de mathématiciens objectifs. Cette affirmation correspond précisément à la modélisation du problème. Les modèles mathématiques sont toujours construits sur de telles suppositions. Les modèles sont bons lorsqu'il n'y pas d'autres facteurs importants qui interfèrent pour décaler les résultats des prévisions, ce qui est le cas pour la Bible à une petite précision près que nous allons expliquer.
Il y a en effet une petite remarque à ajouter : toutes les lettres de la Bible n'apparaissent pas avec la même fréquence. Il y a des lettres plus rares et d'autres plus fréquentes ; c'est pourquoi nous ne pouvons pas dire que la Bible est un livre "moyen" dans lequel chaque lettre devrait apparaître de façon similaire. Ainsi nous allons construire un modèle qui prend en compte cette différence d'apparition des lettres en supposant que la distribution des lettres est hasardeuse autour des fréquences définies pour chaque lettre.
En conclusion, l'une des estimations les plus fondamentales du modèle est que nous accepterons que la Bible corresponde bien à livre "moyen" de notre modèle. En effet, tous nos calculs se feront pour un texte dont les lettres sont réparties au hasard. Pour bien comprendre les résultats, il faudra bien comprendre le sens des phrases de la façon suivante : une phrase comme "l'espérance de trouver le mot 'code' dans la Bible est de 34 000 fois" doit être interprétée de la façon suivante : "en recherchant dans tous les différents livres de 305 000 lettres selon le modèle qui est détaillé dans ce livre, la moyenne d'apparition du mot 'code' est de 34 000 fois". C'est là le sens de toutes les estimations que nous donnerons.
Nous verrons si les découvertes sont extraordinaires ou non. En langage mathématique, on dit que les résultats sont significatifs ou non. C'est-à-dire est-ce que les découvertes faites sont tout à fait normales au regard des prévisions ou bien sont-elles prodigieuses ? .
Du texte hasardeux à la Bible
Difficulté mathématique simple
Comme nous venons de le voir, dans le texte de la Bible les lettres ne sont pas choisies complètement au hasard. En particulier, toutes les lettres ne réapparaissent pas avec la même fréquence. En effet, par exemple la lettre å (la lettre hébraïque Waw) apparaît dans près de 10% des cas, soit environ 1 lettre sur 10, alors que la lettre â (la lettre hébraïque Gimel) apparaît à peu près dans 0.7% des cas, c'est-à-dire environ une lettre sur 145 lettres, ce qui est de beaucoup inférieur. On constate ainsi clairement que les lettres ne sont pas équitablement réparties.
Il serait assez grossier de choisir le modèle simpliste que nous avons présenté parce que celui-ci suppose que les lettres apparaissent dans les mêmes proportions. Les mots faits de lettres rares auraient une estimation nettement surévaluée, alors que les mots fait de lettres courantes seraient nettement sous-évalués. Si l'on étudiait une moyenne sur un ensemble vaste de mots, le modèle simpliste serait suffisant. Comme nous allons étudier l'apparition de certains mots précis, il serait très malvenu de choisir ce modèle.
Il faut adapter le modèle au cas précis qu'on étudie : la Bible. Pour cela, il faut tenir compte de la différence d'apparition des lettres. Nous allons transformer notre modèle de la façon suivante : au lieu d'attribuer à toutes les lettres la même espérance d'apparition de 1 sur 22, nous allons établir une espérance spécifique pour chaque lettre. Cette espérance correspondra à son taux d'apparition. Par exemple, la lettre å qui apparaît une fois sur 10 en moyenne se voit attribuer l'espérance de , la lettre â qui apparaît une fois sur 145 se voit attribuer l'espérance de , etc Etant donné que la somme de toutes les lettres constitue le texte, la somme de leur espérance fera 1.
Ce modèle est plus précis, mais il faut bien comprendre ce qu'il signifie : le modèle suppose toujours que nous allons travailler sur des textes hasardeux, mais dont les lettres apparaissent dans une certaine proportion définie. Les résultats que nous obtiendrons devront donc être compris de la façon suivante : si un mot a pour espérance 15, cela signifie qu'en recherchant ce mot dans tous les textes hasardeux (ayant ses fréquences de lettres définis par les fréquences du texte biblique) alors la moyenne serait de 15 apparitions par texte_ On en conclut naturellement que si le texte biblique est bien mélangé, il est fort probable d'y trouver environ 15 fois le mot.
L'espérance d'un mot
Difficulté mathématique assez faible
Il faut adapter les formules que nous avons trouvées sur le nouveau modèle. En fait, la transformation à effectuer n'est pas très compliquée. L'estimation du nombre de positions (donnée par la formule un peu complexe des pages précédentes) reste inchangée. Quelles que soient les lettres du texte, un mot de 4 lettres aura toujours environ 15 500 000 000 milliards de positions possibles dans un texte de 305 000 lettres. La seule nouveauté porte sur l'espérance des lettres.
L'espérance des lettres est plutôt facile à exprimer. Prenons toujours l'exemple du mot 'code' que nous allons hébraïser phonétiquement pour coller au texte biblique. La lettre 'c' ou le 'ë' en hébreu (le kaph) a une espérance de 1 chance sur 25.5 lettres, le 'o' ou le 'å' en hébreu (le waw, la correspondance n'est pas tout à fait naturelle) a une espérance de 1 chance sur 10, le 'd' ou le 'ã' en hébreu (le daleth) a une espérance de 1 chance sur 43.5 lettres, et le 'e' ou le 'ò' en hébreu (le ayin : il n'y a pas exactement de correspondance en hébreu, c'est un choix arbitraire) a une espérance de 1 chance sur 27.1. L'espérance d'obtenir ces quatre lettres 'ëåãò' a une position précise est le produit des quatre espérances énoncées, soit :
1/25,1 x 1/10 x 1/43,5 x 1/27,1= 1/300607. Ceci est l'espérance d'obtenir le mot 'code' (qui n'a pas de sens en hébreu) pour n'importe laquelle des positions possibles.
L'espérance d'obtenir ce mot dans le texte est donnée par le calcul suivant :
15 500 000 000 x 1/300607 = 51562 qui est le produit du nombre de positions possibles par l'espérance d'apparition du mot. Ce nombre est l'espérance d'apparition du mot 'code' (traduit lettre à lettre en hébreu). Ce mot risque d'apparaître autour de 50 000 fois dans le texte biblique.
De cet exemple, on peut tirer une formule générale pour n'importe quel mot dans n'importe quel texte. L'espérance est donnée par le produit du nombre de positions possibles pour un mot multiplié par l'espérance d'apparition de ce mot à un endroit précis. C'est-à-dire pour un mot de longueur m, un texte de longueur T.
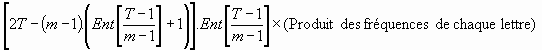
Dans cette formule, on retrouve le premier facteur, le plus élaboré, qui estime le nombre de position ; par contre, le second facteur est nouveau, c'est lui qui prend en compte la spécificité de chaque lettre du mot étudié.
Ce résultat que nous venons de trouver représente l'espérance de trouver un mot donné, par le moyen du saut de lettres, lorsque celui-ci est codé dans le sens de la lecture ; mais comme nous l'avons vu les mots peuvent aussi être codés à l'envers. Il suffit de multiplier par deux le nombre de positions possibles pour en obtenir le nombre total, car chaque position à l'endroit correspond aussi à une position à l'envers. On en déduit la formule suivante :
L'espérance de trouver un mot, à l'endroit ou à l'envers, dans un texte par le procédé du saut de lettre est donc :
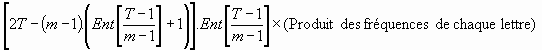 - - m le nombre de lettre du mot cherché
- - m le nombre de lettre du mot cherché
- T la taille du texte
C'est la formule finale que nous utiliserons dans toute notre recherche pour estimer l'apparition d'un mot à l'intérieur du texte Biblique.
Pour pouvoir exploiter cette formule, il suffit juste de connaître l'espérance d'apparition de chaque lettre hébraïque dans la Bible. L'ensemble de ces résultats est consigné dans un tableau que voici :
|
Lettre |
Lettre |
Espérance |
Une lettre sur |
|
ALPEH |
|
0.0887 |
11.3 lettres |
|
BETH |
|
0.0536 |
18.7 lettres |
|
GIMEL |
|
0.0069 |
144.6 lettres |
|
DALETH |
|
0.0231 |
43.4 lettres |
|
HE |
|
0.0920 |
10.9 lettres |
|
WAW |
|
0.1003 |
10 lettres |
|
ZAIN: |
|
0.0072 |
138.8 lettres |
|
RETH: |
|
0.0236 |
42.4 lettres |
|
THET |
|
0.0059 |
169 lettres |
|
YOD: |
|
0.1036 |
9.7 lettres |
|
KAPH |
|
0.0392 |
25.5 lettres |
|
LAMED |
|
0.0707 |
14.1 lettres |
|
MEM |
|
0.0823 |
12.2 lettres |
|
NUN |
|
0.0464 |
21.6 lettres |
|
SAMECH |
|
0.0060 |
166.2 lettres |
|
AYIN |
|
0.0369 |
27.1 lettres |
|
PHE |
|
0.0157 |
63.5 lettres |
|
TSADE |
|
0.0130 |
76.8 lettres |
|
QOPH |
|
0.0154 |
64.9 lettres |
|
RECH |
|
0.0595 |
16.8 lettres |
|
CHIN |
|
0.0511 |
19.6 lettres |
|
TAV |
|
0.0589 |
17 lettres |
|
Du même auteur : | ||||
| Connexion privée | Contact | Proposer de l'aide | Signaler un problème | Site philosophique flexe |

