Distribution de Fibonacci

Quelle est la meilleure distribution des graines dans une fleur ?

Nom du logiciel : Distribution de Fibonacci
Version : 1.0
Environnement : Window Xp à Win10
Taille : 392 Ko
Langue : Français
Année de lancement : 2017-2023
Editions : Mike°Soft (C)
Licence : Usage gratuit
Logiciel ayant trait aux thèmes : Math -  Complexité -  Education -  Enseigner_les_maths

Certains travaux mathématiques montrent que la distribution des graines de tournesol ou des ecailles de pommes de pins suivent une loi mathématique extrêmement précise.
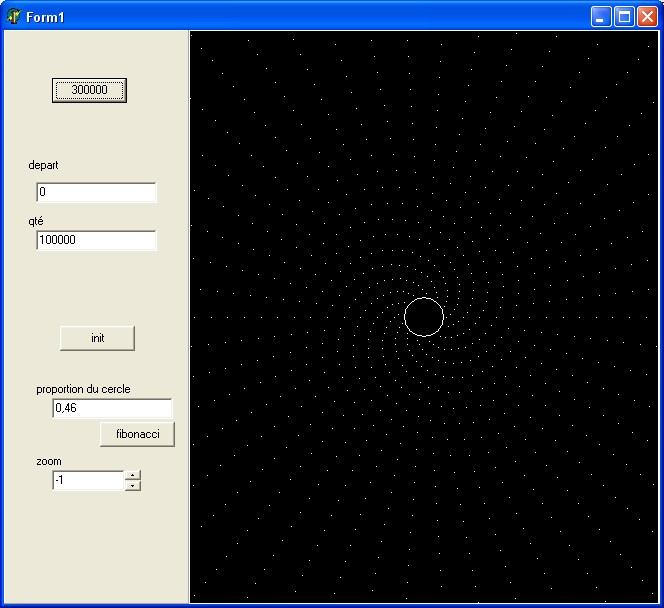
L'idée proposée est que le meilleur angle pour faire pousser les pépins est la proportion (nombre d'or=1.61803... qui revient à 0.61803...) du cercle.

Il se trouve que c'est aussi la limite de la suite des quotients successifs de la suite de nombres de Fibonnacci ( 1, 1, 2(=1+1), 3(=2+1) ,5(=3+2),8(=5+3),... donnant les quotients 1,2,3/2,5/3,8/5,... qui se rapproche vite vers le nombre d'or)

Cela permet une distribution qui en s'éloignant (quand la plante pousse) occupe au mieux un espace plan.
En effet quand on choisit mal un angle, il se crée "des lignes" qui utilise une distribution non homogène de l'espace.

.

 

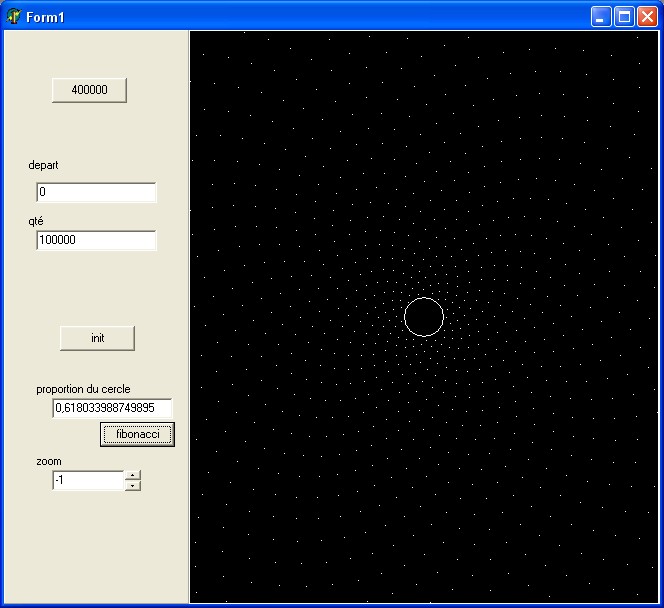
Certaines justification mathématiques établissent que le nombre d'or est la proportion idéale (du tour compet) pour l'angle qui sépare les grains successifs.
(en comparant fraction continues et fraction rationnelle p/q dans la recherche du moindre reste fractionnaire on trouve assez naturellement 1/(1+1/(1+1/(1+...)))) qui est le nombre d'or)
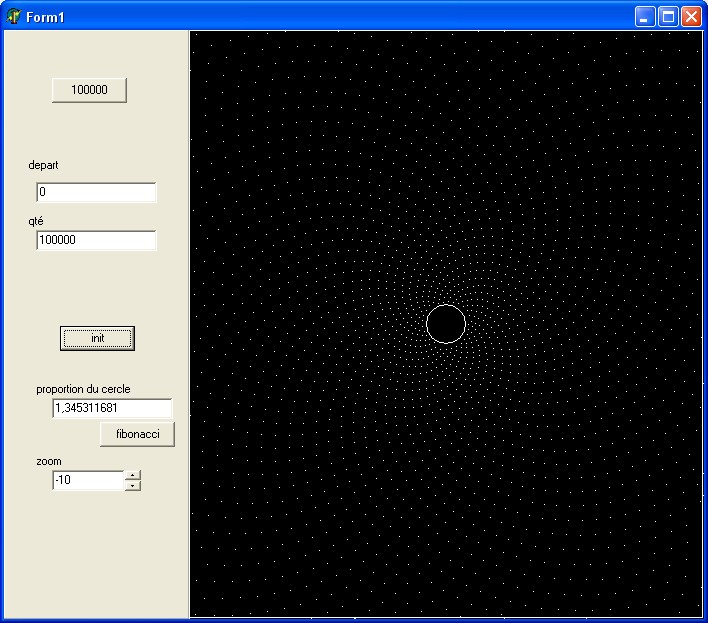
Si la justification semble correcte, est-ce vraiment une nécessité? N'y a-t-il pas une infinité d'autres angles qui occupent aussi "presque tout l'espace de façon homogène" ?